Introduction
The prior article introduced us to the Living Algorithm’s Family of Derivatives. In Living Algorithm System we suggested that a trio of these measures generate a predictive cloud that is important for pattern recognition. This article zeros in on this trio of ongoing measures – examining them from a mathematical perspective. Specifically, we are going to see how one of these measures, the Living Average, indicates the contextual velocity of the data stream, while another of these measures, the Directional, indicates the data stream’s contextual acceleration.
Differentiating Velocity & Acceleration of Crucial Relevance to Study
Differentiating velocity and acceleration is relevant to this study for at least three crucial reasons. 1) This differentiation is the manner in which random noise is discerned from meaningful input. 2) Info acceleration is the basis of our theory of attention that is at the heart of learning. 3) Velocity and acceleration are concepts that link the dynamics of information with the dynamics of matter.
Newtonian Constructs bridge Matter & Life?
This final reason has special relevance. In another article we made the claim that 'Exploded' Newtonian Constructs bridge the domains of matter and life. Velocity and acceleration are at the heart of the concepts of force, work and power. These crucial Newtonian constructs are fundamental to the dynamics of both material and information systems. Understanding the dynamics of information is crucial to understanding why the Living Algorithm lies at the heart of the human experience.
Committed to Accessible Mathematics
If all this talk about these strange mathematical concepts is disturbing, don’t worry. We are going to be discussing velocity and acceleration with some common every day examples to familiarize us with the concepts. And the minimal mathematics is visual rather than conceptual. We remain committed to our pledge of rendering the Living Algorithm mathematics accessible to the intelligent public.
The Mathematics of Data Stream Velocity & Acceleration
Repetition to reinforce memory: The current article focuses upon how velocity and acceleration apply to the Living Algorithm’s Info System. This Info System is based upon the Living Algorithm’s method of processing information – data streams in particular. In her general form she generates an entire Family of ongoing central measures from an ongoing Stream of Raw Data. These Measures determine crucial features of any flow of numerical information. One of these measures, the Living Average is the contextual velocity of a data stream. Another of these measures, the Directional, is the contextual acceleration. Let’s take a brief look at the mathematics behind these assertions.
Living Algorithm generates contextual velocities and accelerations
Let's begin our discussion with a simple verbalization of how the Living Algorithm transforms Raw Data into Velocities and Accelerations. The Living Algorithm digests the Raw Data from any stream of information to generate another data stream. This is the ongoing Living Average. She represents the contextual velocity of the data stream. A data stream of differences (rate of change) between the Raw Data and the Living Average is a byproduct of this process. The Living Algorithm digests this data stream to generate yet other data streams, which represent contextual accelerations. One of these contextual accelerations, the Deviation, is a sheer magnitude, while the other, the Directional, is a directed vector with magnitude. We can employ the same technique to generate an endless stream of higher level Directionals and Deviations. For the curious, the following provides a mathematical summary that will demonstrate the basic principles and correspondences. (A complex discussion of these topics is included in the Data Stream Momentum Notebook.)
Cell Equation generates Living Average - a contextual velocity
The Living Algorithm can also be written in the format below.
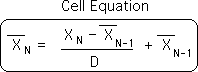
In essence, this equation generates a way of organizing information that we choose to call Living Averages (sometimes called Decaying 'Memory' Average in the literature of science). In the days before personal computers, the Author employed this equation to compute endless decaying averages. The Living Average is a central measure that represents the contextual velocity of the data stream. The importance of the contextual velocity is that it enables us to constantly adjust averages as we move through time. The following definition allows us to rewrite the equation in yet another form – as a rate of change (indicated by the triangle ∆).
![]()
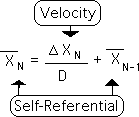
The following version of the Living Algorithm reminds us of her self-referential nature, as well as emphasizing the innate nature of the Living Average as a velocity.
The Directional as a contextual acceleration
Although it took decades, we were surprised to find that the logic behind the same Living Algorithm that generated the Living Average also generated the Directional. The equation for the First Directional is shown below. (We can employ the same technique to generate an endless stream of higher level Directionals.)
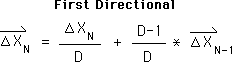
Mathematically these averages of change (Directionals, et al) represent different levels of acceleration. Understanding the difference between acceleration and velocity is essential to the understanding of the contribution of Newtonian Physics to this branch of information theory
Everyday notions of Velocity & Acceleration
We've likened Living Algorithm Measures to the traditional notions of velocity and acceleration. Let’s refresh our memory as to what these everyday concepts mean. Velocity is a speed. Speed is the rate of change of location over time. For example, the speed of 60 MPH means that in one hour that the location changes by 60 miles. Acceleration, on the other hand, is the rate of change of a velocity over time. For example, as we accelerate to get on the freeway our velocity may change from 0 MPH to 60 MPH in 10 seconds. As velocity is also a rate of change, acceleration is the rate by which the velocity, a rate of change, changes.
Directional = Rate of Change of the Rate of Change (to the 2nd Power)
We’ve shown that the Living Average is a velocity. Specifically she could be called the average speed (the velocity) of the data stream over time. In similar fashion, the Directional is the average speed of the Living Average over time. As such, the Directional is the acceleration of the data stream. As an acceleration, the Directional is the rate by which a rate of change, changes (the rate of change to the 2nd power - the triangle squared). This is shown in the equation below.
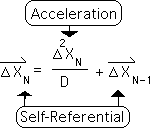
Incredible Self-Referential complexity of Directionals
Let it be noted that the Directional adds yet another layer of self-referencing. This self-referencing multiplies the complexity of the interaction. To compute the Directional we need the most recent data point, as well as the prior Living Average and the prior Directional. This is shown in the equation below.
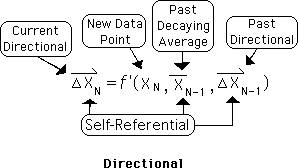
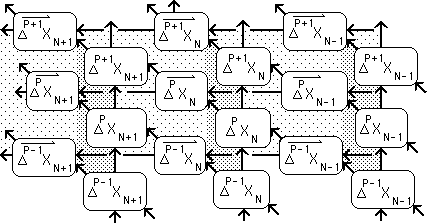
As we move through time, creating new data points in our ongoing living data streams, this self-referential process is repeated ad infinitum. The following diagram is visual illustration of the complexity of this unique process. It is also a representation of an ongoing series of moments.
Data Stream Velocity & Acceleration in relation to Space & Time
The velocity and acceleration of an object, such as a car, makes practical sense. But what does it mean to be the velocity or acceleration of a data stream?
Physical Velocity & Acceleration require Space & Time
Physical velocity (speed) is the change in location over time. A simple computation for speed is the distance traveled divided by the amount of time expended (d/t). For instance, if it takes 2 hours to drive to Los Angeles, which is 100 miles away, the average speed for the journey would be 50 MPH (traffic must have been bad). Physical acceleration is the change in velocity over time. To compute both of these measures (velocity and acceleration) both space and time are required.
Info Time = Duration between Living Algorithm Iterations (Repetitions of the Process)
In a data stream, each point is separated from the next by an increment of ‘time’, T. Although T is not part of the Living Algorithm, it is inherent to the notion of an ongoing flow of discrete data points. T represents the amount of ‘time’ between successive data points. In terms of the Living Algorithm, T is the amount of ‘time’ between each iteration (each repetition of her data digestion process).
How the Analog Physical Matrix and the Incremental Information Matrix interact with Time
Time is placed in quotes because we are speaking about information flow. The physical and information matrices interact with time in different ways. Interaction between the physical world and time is analog (continuous). Because a stream of information is necessarily comprised of distinct data points for digestion purposes, the interaction between an information digesting system and ‘time’ is segmented in nature. Time is the same in both systems. It is the way that the particular system interacts with time that creates the difference. Because living systems must digest data streams to survive, their information processing system also requires a segmented interaction with time.
How the Physical & Information Matrices interact with Space
Physical dynamics and info dynamics both deal with rates of change. Inherent to change is the necessity of the state of something changing over time. For convenience, we will refer to this ‘state’ change as a change of location in space. The physical matrix (with the exception of the subatomic realm) interacts with both space and time in an analog (continuous) fashion. The information matrix, as defined by the Living Algorithm, interacts with changes over time in a incremental fashion. With each repetition of the Living Algorithm process, a distinct and separate data point is computed. This is quite different from the analog physical world, where there is no space between data points. Reiterating, the physical matrix has an analog relationship with space and time, while the information matrix has an incremental relationship. We will explore the differences between the two systems and the ramifications in more depth in future articles.
Relevance of Velocity & Acceleration in a Data Stream
At the beginning of this article, we mentioned that differentiating velocity and acceleration is significant to the Living Algorithm System for three crucial reasons. Following is a brief introduction to these important issues. Future articles will explore these topics in more depth.
Differentiating noise from meaning
Noise versus Meaning
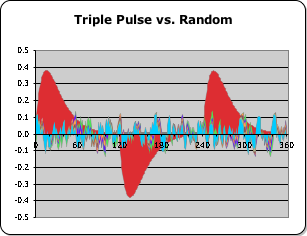
1) It is possible to differentiate background noise from a meaningful signal by examining a data stream’s acceleration. The acceleration of a meaningful signal is significantly greater than the acceleration of a random data stream. This is shown in the following graph, which compares the accelerations of these two types of signals. The red area represents the organized signal, and the multi-colored area, the random signal. In contrast a data stream’s velocity reveals nothing about this crucial difference.
Attention is attracted to a Data Stream's Acceleration, not its Velocity.
2) It is important to be able to differentiate info velocity from info acceleration regarding Attention, as defined in the Living Algorithm System. As we have suggested, the acceleration of a data stream is an excellent indicator of whether a data stream has significance to the organism – noise or a potentially meaningful signal. Conversely, the velocity of a data stream yields no such criterion. Accordingly, Attention, for pragmatic reasons, is attracted to data stream acceleration, but not velocity. This feature of Attention has important ramifications, when we explore the relationship between Learning and the Living Algorithm System.
Velocity & Acceleration at the Heart of Data Stream Dynamics
3) The notions of velocity and acceleration in a data stream are crucial because they are at the heart of Data Stream Dynamics. This dynamical system is based upon the Newtonian constructs of Force, Work, and Power, as applied to the flow of information. Data Stream Dynamics provides the causal mechanism that links the Living Algorithm System with behavioral reality.
Data stream dynamics? The words sound fascinating, but require a more thorough description. This elaboration is coming in the following articles.
The importance of Data Stream Velocity & Acceleration
Data Stream Acceleration: Random Data Stream Low – Organized Data Stream High
Let’s summarize our findings to facilitate understanding. Velocity is the first level of change, while acceleration is the second level. Understanding the difference between the velocity and acceleration of a data stream is important for a variety of reasons. A data stream's acceleration can be employed to make a preliminary check as to whether the data stream is random or organized. A random data stream's rate of acceleration is the lower of the two. In contrast, a data stream's velocity provides no such information regarding whether a data stream is random or not.
Attention focuses upon Data Stream Acceleration to weed out Random Data Streams
Living systems, we theorize, don't want to waste the valuable energy of Attention upon random data streams. Therefore, Life focuses the mental energy of Attention on a data stream's acceleration to make the determination as to whether a data stream is random or not. In contrast, Attention disregards data stream velocity, as it doesn't provide this crucial information. Evidently, this feature becomes very important when it comes to understanding the primacy of Attention in our theory linking the Living Algorithm System with Life.
Data Stream Dynamics provides understanding of the Living Algorithm's Transformations
This cursory exploration illustrates how velocity and acceleration are foundational to the Data Stream Dynamics of the Living Algorithm System. Understanding the dynamics of data streams is significant because this leads to an understanding of the forms of information digestion. Due to the primacy of information digestion in the realm of perception, we theorize that the forms of information digestion are of crucial importance in the emergence of the living systems. If the Living Algorithm is the language of living information digestion, as we suggest, these forms represent the innate grammar of the system. The Pulse of Attention and the Triple Pulse are just a few examples of the Living Algorithm’s forms or transformations. We theorize that the dynamics behind these transformations links the behavior of the two systems, mathematical and biological.
1st Volume establishes Correspondences; 2nd Volume establishes Plausibility
The 1st volume, Triple Pulse Studies, certainly provided an abundance of evidence from myriad disciplines indicating the patterns of correspondence between the two systems. The 2nd volume illustrated that the Living Algorithm, at least, fulfills some essential requirements of a data stream mathematics of living systems. In the investigation, none of our findings contradicted our theory that the Living Algorithm could be one of the primary methods by which living systems digest information. Could the Living Algorithm even be a candidate for the position as the elemental cell of data digestion?
Current Volume attempts to provide Causal Mechanism via Dynamics
In fact, this series of article streams is devoted in part to supporting this proposition. The 1st volume established the patterns of correspondences; the 2nd volume established the plausibility of the above theory. The current volume, the 3rd, attempts to provide a plausible causal mechanism for the linkages between the two systems. To this effect, the article stream attempts to link the dynamics of information to the dynamics of matter. The Author establishes this linkage by indicating the symmetries between material dynamics and Data Stream Dynamics – hence the name of the volume.
Time to explore Data Stream Space & Time
To achieve this formidable task, he must ‘explode’ the traditional constructs of Newtonian Physics. This includes the fundamental notions of space, time and matter. The current article provided a preliminary exploration of space and time. The next article explodes these primal constructs to incorporate information into a universal system of dynamics. To continue our fascinating journey, check out the next article in the series – Data Stream Space & Time.