Home Science Page Data Stream Momentum Directionals Root Beings The Experiment
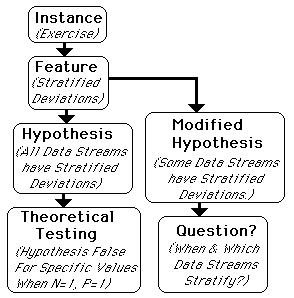
Here we set a context for this exploration of Deviations by attempting to use the same terminology that Ian Stewart and Cohen use in their book, The Collapse of Chaos. Initially we perceived an Instance of Deviations in the Data Stream, Exercise. We perceived a Feature of this Data Stream; its deviations were stratified. We hypothesized a Rule – all deviations in every Data Stream stratify in the same way. Reducing our system to its elemental parts, the data, we immediately found a counter-example, which negated the proposed Rule or Hypothesis. We still had our Instance, however, so we modified our Rule or Hypothesis, to the statement that some Data Streams have Stratified Deviations. This led immediately to the Question of: When & Why do Data Streams Stratify?

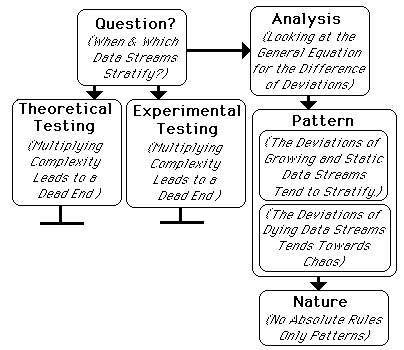
Staying with our elemental parts, we continued searching for some Rule to determine when or why Data Streams stratify. We only found a multiplying complexity but no Rules. We then took the experimental route from the elemental level, hoping to see some patterns, at least, that might predict the Feature that we perceived in our first Instance. Again all we saw was multiplicity but no patterns that would predict the Feature of the Data Stream, Exercise. We then returned to the Pattern that created the system. Here the sub-patterns that predict the Feature, jumped out. The analysis of the content was inadequate to the task of producing General Rules that would produce our Features. Also experimenting on the content yielded a similar Dead End. It was only when looking at the Context of problem, the movement of Data through time that the Patterns, not Rules, of Nature were revealed.
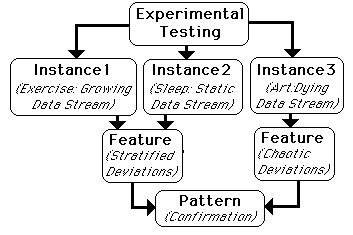
Hence our analysis of our One Rule led to Patterns, which predict Features of Instances. We looked at two more Instances in the Experimental Section and they confirmed the Patterns perceived from the One Rule. We discovered something more about the Nature of the System, but it was not more Rules. It was only Patterns of Behavior.
This system based upon only one Rule, yielded no general Rules. Because we are talking about a contextual system that feeds upon itself, there are no absolutes in this system, only tendencies, patterns. There is no overall Rule that predicts when any individual deviation will be greater or lesser than any other deviation in any given instance. All the Rules perceive is Chaos. There is nothing to hang a General Rule upon.
However in perceiving the system through its Context rather than its Content, Patterns jumped out. Its Content is the Data itself. Its Context is its movement through Time. The equation that generates the Deviations is quite simple but it leads very quickly to overwhelming complexity at the elemental level because it feeds upon itself. So the Content of this system tells us very little about the Nature of the system itself, its Patterns in motion. Our equation is the Rule that tells us how to create the Deviational Derivatives of the Data Stream.
Let us point out that our derivations could generate millions of specific Rules that are fairly useless. Looking at Graph 4, Deviational Differences after 5 points, we can generate quite a few useless rules. If a Continuous Data Stream begins with 10, 10, 1, 10, 0, then no matter what the next Data point is, the first Deviation will always be greater than the 2nd Deviation. With a similar beginning, if the next point is greater than 1.5 then the zeroth Deviation will always be greater than the first Deviation. Or with the same beginning, if the next point is between 8 and 9 then the fifth Deviation will always be greater than the fourth Deviation. And so on and so forth. The Rules multiply easily from this one graph, but they don't congeal into any big rule, because of the system is so contextual. From one Rule come many Rules, but no Patterns. The non-Absolute Patterns only emerge from the analysis of the system in motion, in the context of its Life.
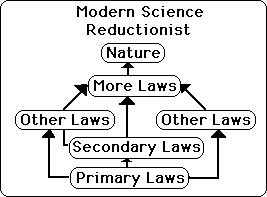
Euclid used elemental postulates to derive Theorems, which were always true if his postulates were true. He used Rules to derive more Rules, which were used as the basis of more Rules, and so forth, in a system with an ever-increasing complexity of structure of Rules.
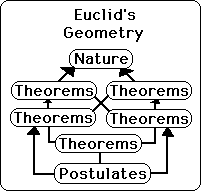
Euclid, in many ways, was a primary inspiration for the development of modern mathematically based science.
We're talking about something else here. In the Deviational System we have one Rule only. It can tell us how to generate every number in the System. But no rule can be derived from the one Rule that will tell exactly when stratification occurs. Instead the Rule leads to a Derivation, which leads to Analysis. The Analysis recognizes the Patterns from a context of movement through time. The Patterns reveal the Nature of the System, its tendencies. The Nature is in no way absolute but only conditional. So our one Rule generates a System, which has a conditional Nature.
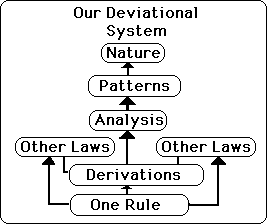
As pointed out above, there are millions of mini-rules that can be generated from the one Rule. These mini-rules don't lead anywhere concrete, however. Whenever an attempt is made to generalize the mini-rules, there are too many exceptions to have any general significance. Here we have a One Rule System which has a Nature filled with contextual Patterns, rather than absolute Rules.