Introduction
The following proof derives the general expressions for the Living Average and the Directional (the 1st and 2nd derivatives) of the Number String data stream. The Number String data stream consists of identical information. For instance, a string of 1s is an individual case of a Number String data stream.
Proof A: The Living Average & Directional written in terms of K, the Scaling Factor
A1. We begin with the Basic Living Algorithm. The Living Algorithm's sole function is to digest data streams. The Basic Living Algorithm's digestion process generates the data stream's 1st derivative, known fondly as the Living Average.
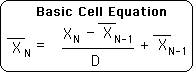
A2. A straightforward algebraic procedure, i.e. separating out factors, yields this version of the same equation.
![]()
A3. K, the Scaling Factor, has the following definition.
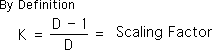
A4. Substituting K for the equivalent algebraic expression in Equation A2 yields the following equation for the Living Average. This is the form of the Living Average Equation that we will employ in the following proofs.
![]()
A5. The Living Algorithm's algorithm is employed to generate all the data stream derivatives, not just the 1st derivative (the Living Average). Following is the standard equation for the data stream's 2nd derivative (the Directional). The arrow indicates that it is a vector.
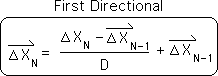
A6. We employ the same algebraic manipulations and substitutions that were used above to arrive at this alternate representation of the Directional.
![]()
A7. The 1st term on the right side of the equation has this definition.
![]()
A8. Substituting this expression into Equation A6 yields the following expression. This is the operating equation that we will employ for the data stream's 2nd derivative – the Directional Equation.
![]()
Proof B: Number String's Living Average & Directional for the 1st point (N=1)
B1. Definition: A Number String is a data stream, whose elements are identical. The following algebraic expression symbolizes this condition.
![]()
B2. Since all the elements are identical, we choose to represent each element in the stream by the letter A. A can be any type of information, including non-numerical, as we shall demonstrate.
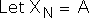
B3. Let's assume that our Information System begin the process at 0. This means that both the Living Average and the Directional (the data stream's 1st and 2nd derivatives) equal 0. These are the initial conditions of the Living Algorithm's iterative process. This is also known as 'zeroing out' or 'taring' the system of any momentum (discussed in more depth elsewhere).
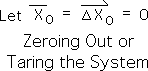
B4. Summarizing, the Number String data stream consists solely of As and the System starts at 0. Let's see what happens Living Algorithm's Living Average digests this data stream – point by point. We begin the process with the 1st data point, X1. Substituting X1 for XN in the Living Average's operable equation (Eq. A4) yields the following expression.
![]()
B5. The prior Living Average, X0 bar, equals 0 by assumption (Eq. B3). This substitution is shown in the following equation.
![]()
B6. Zero multiplied by any term equals 0. As such, the last term drops out of the equation. Employing our knowledge that all the Data points equal A (Eq. B2) yields the following result. The first Living Average, X1 bar, always equals A/D: A, our information packet, whatever it consists of, divided by D, the Decay Factor.
![]()
B7. Let us perform the same procedures to uncover the data stream's 2nd derivative, the Directional, X1 arrow, for the 1st data point, X1. We substitute 1s for Ns in the Directional's operable equation (Eq. 8a) with the following result.
![]()
B8. We know that the values of the initial Living Average and Directional are 0 by assumption. Substituting these known values into the above equation yields:
![]()
B9. As they don't contribute anything, the zero terms drop out of the above equation. This gives us the general expression for the 1st data point's Directional, X1 arrow. Surprise of surprises, it is the same as the 1st data point's Living Average. In both cases, it is A/D.
![]()
We will employ these results to compute the Living Average, X2 bar, and the Directional, X2 arrow, for the 2nd data point, X2.
Proof C: Number String's Living Average & Directional for the 2nd point (N=2)
C1. To uncover the expression for the 2nd data point's Living Average, X2 bar, we first substitute X2 for XN in the Living Average's operable equation (Eq. A4). This yields the following expression.
![]()
C2. All the data points in the Number String data stream equal A. Therefore X2 also equals A. From Equation B9, we also know the expression for X1 bar. Substituting these values in the above equation results in:
![]()
C3. Factoring out A/D provides us with the desired result, the algebraic expression for the Living Average of the 2nd data point, X2 bar.
![]()
C4. To derive the expression for the 2nd data point's Directional, X2 arrow, we first substitute X2 for XN in the Directional's operable equation (Eq. A8). This yields the following expression.
![]()
C5. Equation B9 provides the values the prior Living Average and Directional, X1 bar and X1 arrow. Plus all the data points, hence X2, equal A. We perform to substitutions to get the following expression.
![]()
C6. We factor out the familiar A/D term to come up with:
![]()
C7. Performing a straightforward algebraic manipulation we see that the first two terms after the parenthesis equal K, the Scaling Factor.
![]()
C8. We substitute K for the more complicated expression.
![]()
C9. Combining terms provides the algebraic expression for the 2nd data point's Directional, X2 arrow, our stated goal.
![]()
Again we will be employing these results when we examine the 3rd data point's 1st and 2nd derivatives – the Living Average, X3 bar, and the Directional, X3 arrow.
Proof D: Number String's Living Average & Directional for the 3rd point (N=3)
D1. In our quest to identify pattern, let us now derive the Living Average and Directional (the 1st and 2nd derivative) for the 3rd data point in our Number String data stream. To derive the expression for the 3rd data point's Living Average, X3 bar, we first substitute X3 for XN in the Living Average's operable equation (Eq. A4). This yields the following expression.
![]()
D2. All the data points in the Number String data stream equal A by definition. Therefore X3 also equals A. From Equation C3, we also know the expression for X2 bar. Substituting these values in the above equation results in:
![]()
D3. Factoring out the increasingly familiar A/D term provides us with the desired result, the algebraic expression for the Living Average of the 3rd data point, X3 bar.
![]()
D4. To derive the expression for the 3rd data point's Directional, X3 arrow, we first substitute X3 for XN in the Directional's operable equation (Eq. A8). This yields the following expression.
![]()
D5. Equation C3 provides the value for the prior Living Average, X1 bar, and Equation C8 provides the value for the prior Directional, X2 arrow. Plus all the data points, hence X3, equal A. We perform to substitutions to get the following expression.
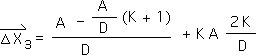
D6. We factor out the same A/D term to come up with:
![]()
D7. Let's simplify the first two terms after the parenthesis. We first break the fraction into parts. Equation C7 exhibits that the first 2 terms in the resultant equation equals K, the Scaling Factor. This equivalence is exhibited in the final expression.
![]()
D8. We factor out K from the final expression. We again come up with the 1 - 1/D term that equals K (Eq. C7). Multiplying the two factors together yields K2.
![]()
D9. We substitute the result from Equation D8 into Equation D6.
![]()
D10. Combining terms provides the algebraic expression for the 3rd data point's Directional, X3 arrow, our stated goal.
![]()
Proof E: General Expression – Number String's Living Average
E1. Patterns are emerging. Following is a list of the Living Averages (the 1st derivative) for the first 3 data points in our Number String data stream.
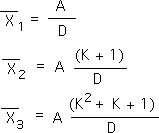
E2. The pattern seems fairly obvious. With each successive data point a K with a higher exponent is added to the string. From these particulars we induce the general expression shown below.
![]()
E3. However, the perception of a pattern doesn't establish its truth. To test the validity of the above equation as a general expression for the Living Average of any point, XN, in the Number String data stream, we must apply the Induction Principle. This important principle is defined in the following box.
"Induction Principle. A statement Q(n) about the integer n is true for all positive integers n if
1. Q(1) is true.
2. For each integer n, the truth of Q(n) implies the truth of Q(n+1); that is, if Q(n) is true then Q(n+1) is true.
The truth of Q(n) is often called the induction hypothesis, since it is the hypothesis of the implication of property 2." (Burton W. Jones, An Introduction to Modern Algebra, 1975, p. 132)
E4. Equation E2, the general Living Average, is our statement Q(n). We've already satisfied the first condition that 'Q(1) is true'. In fact, we exhibited that Q(1), Q(2) and Q(3) are all true. Indeed, we generated our general equation to fit the recognized pattern of these initial Living Averages.
E5. Now let's see if our general expression can satisfy the second condition: 'if Q(n) is true then Q(n+1) is true'. Our Q(n) is the Number String's Living Average of the Nth point, XN bar (Equation E2). We assume this expression Q(n) to be true. Does Q(n) imply that Q(n+1) is also true? If it does, then the following equation must be true, because this is the expression for the N+1 point, Q(n+1), in the number series generated by the function Q(n). Let's see if the underlying logic of the function generates the following equation.
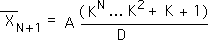
E6. We restate our general equation for the Living Average of any data stream (Equation E4).
![]()
E7. We substitute N+1 for N, to obtain:
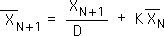
E8. The above expression is the Living Average for any data stream. In this discussion, we are only interested in the Number String data stream, where all elements, XN, equal A. As such, XN+1 also equals A. For the purposes of this proof, we have assumed that Equation E2, a general expression for Number String's Living Average (XN bar), is true. We make these substitutions (A for XN+1 and Equation E2 for XN bar, to obtain:
![]()
E9. We factor the A/D term out of the equation's 2nd expression.
![]()
E10. We further factor out the A/D term from the entire equation and combine terms. This yields the following equation (Equation E5). This is the equation we were trying to prove. This satisfies our 2nd condition: Q(n) implies Q(n+1). It is evident that the function's underlying logic generates the next value in the sequence.
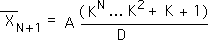
E11. Because our expression satisfies both conditions of the Induction Principle, we can safely assume that Equation E5 is true for any integer, N. In other words, the following equation, a restatement of Equation E5, is the general expression for the Living Average of any data point in the Number String data stream. This is Theorem E, the formula for the Number String’s Living Average, the 1st derivative.
![]()
Proof F: General Expression – Number String's Directional: Part I
F1. That wasn't too bad. Let's see if we can identify any more patterns. Following is a list of the Directionals (the 2nd derivative) for the first 3 data points in our Number String data stream.
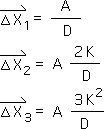
F2. Again the pattern seems fairly obvious. With each successive data point, the K's exponent increases by 1 and the coefficient also increases by 1. The A/D factor remains constant throughout. From these particulars, we induce the general expression shown below.
![]()
F3. While induction can be an effective method of pattern recognition, induction by itself doesn't establish truth. To test the validity of the above equation as a general expression for the Directional of any point, XN, in the Number String data stream, we must apply the Induction Principle enunciated above.
F4. Equation F2, the general Directional, is our general statement Q(n) concerning integers. We've already satisfied the first condition that 'Q(1) is true'. In fact, we exhibited that Q(1), Q(2) and Q(3) are all true. Indeed, we generated our general equation to fit the recognized pattern of these initial Directionals.
F5. Now let's see if our general expression can satisfy the second condition: 'if Q(n) is true then Q(n+1) is true'. Equation F2 above, the general Directional, XN arrow, is the Q(n) in this case. If this statement is true, is Q(n+1) also true? We plug N+1 into the general equation Eq. F2 to determine our Q(n+1) – shown below.
![]()
Does Q(n) imply Q(n+1)? More specifically, does Eq. F2 imply Eq. F5? Let's see.
F6. We restate our general equation for the Directional at any point in any data stream (Equation A8 above).
![]()
F7. We substitute N+1 for N in this equation, to determine the Directional for the N+1 data point.
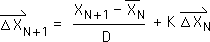
F8. However, we are not investigating all data streams. We are restraining our investigation to the Number String data stream, in which all the elements are equal to A. Hence, XN+1 also equals A. Further Equation E9, just proved, provides the general expression for the Number String's Living Average, XN bar. Plus for the purposes of this proof, we have assumed that Equation F2, the algebraic expression for the Number String's Directional, XN arrow, is true. We make these three substitutions in the prior equation, Eq. F7, to obtain the following result.
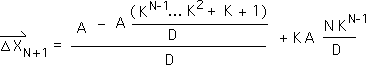
F9. As before, we factor the ubiquitous A/D factor out of the right hand side of the equation to obtain:
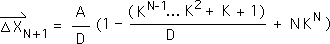
F10. The initial and final terms on the right hand side of the equation are just as we expected. However, it is not evident how the middle terms combine with the rest to achieve the desired result. Let's conduct an independent investigation of these ambiguous middle terms to see what it reveals. We need an intermediate proof.
Proof G: Supplementary Proof - the Middle Term
G1: In previous proofs, we have had to deal with these same middle terms. When we derived the equation for Number String's Directional for the 2nd and 3rd point, we came up with these simplifications for these middle terms – Equations C7 and D8.
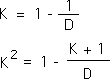
G2: From these particulars, we induce the following equation. This is a general statement about the innate nature of integers.
![]()
G3. Induction, while identifying patterns, does not establish truth. To test the validity of the above equation as a general statement about integers, we must apply the Induction Principle enunciated above.
G4. Equation G2 is our general statement, Q(n), concerning integers. We've already satisfied the first condition that 'Q(1) is true'. In fact, we exhibited that both Q(1) and Q(2) are true – Equation G1. Indeed, we generated our general equation to fit the recognized pattern of these initial cases.
G5. Now let's see if our general expression can satisfy the second condition: 'if Q(n) is true then Q(n+1) is true'. Equation G2 is the Q(n) in this case. If this statement is true, is Q(n+1) also true? We plug N+1 into the general equation Eq. F2 to determine our Q(n+1) – shown below.
![]()
G6. Using standard algebraic procedures, we first break the fraction into 2 parts.
![]()
G7. Equation C7 indicates that the initial 2 terms equal K. We make this substitution.
![]()
G8. We now factor the K out of the expression to obtain the following result.
![]()
G9. If Equation G2 is true, as we assumed it to be, the second factor on the right hand side equals KN. We multiply through, i.e. add exponents, to confirm that the right and left hand sides of our equation are equivalent. In other words, Q(n) implies the truth of Q(n+1).
![]()
G10. Because our general statement about integers, Equation G2 shown below, satisfies both the individual and general conditions of the Induction Principle, we can assume that it is true for any integer, N.
![]()
Conclusion Proof F: Directional for any point in the Number String Data Stream
F9. We made a general statement about integers, the General Expression for the Number String's Directional at any point in the data stream. We fulfilled the individual conditions for this statement. We were attempting to fulfill the general requirements of the Induction Principle when we were stymied by the following equation. Now that we have simplified the middle terms of the following expression, we can conclude our proof.
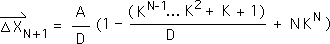
F10. We substitute the results from Equation G10 into the above expression.
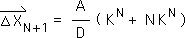
F11. We combine terms to achieve the desired result – Equation F5. In other words, when we assume the general expression for the Number String's Directional to be true, it implies that this statement also holds true for the next Directional in the stream. In even more general terms, Q(n) implies Q(n+1).
![]()
F12. Because our general statement about integers, Equation F2 shown below, satisfies both the individual and general conditions of the Induction Principle, we can assume that it is true for any integer, N. In other words, the following expression provides the Number String's Directional at any point, N. This is Theorem F, the formula for the Number String’s Directional, the 2nd derivative.
![]()
Summary
In summary, this article provides a proof for the general expression (Eq. E10) for the Living Average, the 1st derivative (XN bar), of any point in the Number String data stream (below left) – Theorem E. It also provides a proof for the general expression (Eq. F12) for the Directional, the 2nd derivative (XN arrow), of any point in the Number String data stream (below right) – Theorem F.
![]()
![]()
What is the significance? What do these theorems reveal? For some answers, check out the next article in the stream – Number String Implications.