Section Headings
Posner’s Attention Model: Attention’s Role regarding Sensory Information
Attention Network requires Data Streams to accommodate Choice
Living Algorithm: Open, Immediate, Interconnected & Possibility of Choice
Predictive Descriptors, Dynamic Context & Essential Content
Random Filter, Correlations & Focus Regulation
Simple Arithmetic Computations & Minimal Memory Requirements
Inherent Limitations of Traditional Mathematical Systems
Synopsis
Is there any evidence that Life employs the the LA via Attention to impart Meaning to data streams, the informational food of living systems? Posner's Attention Model has nearly universal acceptance in the scientific community. This article develops the notion that Posner's Attention Model evolved to take advantage of the LA's many talents. (Evolution x Living Algorithm = Posner's Attention Model) This hypothesis has many intriguing implications.
Attention's Mathematical Tool? Certainly a bold claim. What does it entail to be the mathematical tool for Attention?
A lifetime of research on human behavior resulted in a mathematical Theory of Attention. The theory combines attention, information and experience in a simple process-based equation. The Living Algorithm (LA) provides the mathematical foundation for this fresh perspective.
Prior articles examined the unique mathematical features of the Living Algorithm and how its system differs from traditional mathematical systems. The current article explores the LA’s relationship with Attention.
Amazingly, there are multiple patterns of correspondence between the Living Algorithm's mathematical processes1 and Human Attention. They indicate that our cognitive behavior seems to entrain to these processes and that our biological systems related to attention appear to have evolved to take advantage of these same dynamic mathematical patterns.
What is the reason behind these intriguing parallels between the LA’s mathematical behavior and our attention-related behavior – not just cognitive, but biological as well? Does the LA merely provide a mathematical model for the behavior of Attention? Or could it be that the Living Algorithm is Attention’s tool? Is it possible that Attention employs the Living Algorithm as a mathematical interface with the constant flow of environmental information?
The sole intent of this article is to establish the plausibility of this hypothesis.

What are the necessary qualifications for this ongoing mathematical interface? Why is the Living Algorithm even in the running for this incredibly prestigious position? What special features does this deceptively simple algorithm possess that traditional mathematical approaches lack? What are some of the inherent limitations of standard mathematics?
We suggest that a significant feature of this mathematical interface is incorporating the possibility of choice. Mathematics and choice? Putting these two words together is almost an oxymoron. Mathematical systems tend to be viewed as a fixed and automatic. How could choice be associated with a rigid system like mathematics? How is the Living Algorithm able to incorporate choice?
These are some of the questions that this article will attempt to address.
Posner’s Attention Model: Attention’s Role regarding Sensory Information
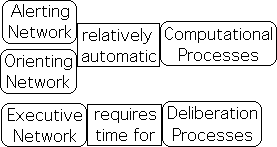
To better understand Attention’s role in human behavior, let us examine the universally accepted Posner Attention Model. According to this model, there are 3 separable, but fully integrated systems located in the brain. These 3 networks are named: Alerting, Orienting and Executive. We will call this interactive complex the Human Attention Network – Attention Network for short, or simply Attention. As a cognitive network, Attention is a process, not an entity.
Let’s see what each network’s function is and how they interact.
Our Alerting Network has two states: Intrinsic Awareness and Phase Alertness. In the Intrinsic Awareness phase, Attention monitors general sensory information from the environment, somewhat like a security guard. If this network identifies an unusual sensory flow, it shifts to the Alertness Phase. The Attention Network’s focus narrows to consider specific, rather than general information. Further, a brain wide alert is sounded and the Orienting Network is engaged. At this point in the process, our sensory apparatus orients towards the source of the unusual information. Activated, the Executive Network evaluates the incoming information and makes a decision as to what action to take, i.e. what adjustment to make to this environmental stimulus.
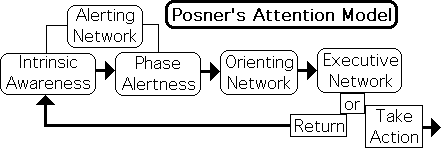
Let us examine the Attention Network’s relationship to the flow of sensory information in more detail. The cognitive process has several salient features.
In the Alerting Network, the focus of Attention has 2 states – general and specific. While in the monitoring phase (Intrinsic Awareness), Attention's focus is in the general state and only notices broad trends of the sensory information flow. If the incoming info is outside the normal range, it is perceived as a stimulus. After the sensory input is labeled as a stimulus, focus shifts from general to specific (Phase Alertness). Attention’s focus narrows to only include the specific sensory information flows associated with the stimulus.
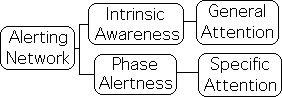
The initial monitoring phase includes evaluating the incoming sensory information flows to determine if they are inside or outside of the norm – usual or unusual – a stimulus or not. If they are within the normal range, the focus remains at a general level. When in the general state of Intrinsic Awareness, the Attention Network seems to act as an information filter.
After a stimulus is identified, focus narrows and the Attention Network engages as many senses as possible, presumably to analyze the specific features of the incoming information (Orienting Network). When in the specific state, the Attention Network seems to analyze the sensory information in greater detail.
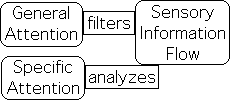
At rest during the ‘monitor’ phase, the brain’s decision-making center (Executive Network) is only activated after Attention identifies sensory information as unusual – a stimulus. With a more detailed analysis of the stimulus provided by specific Attention, the Executive Network attributes meaning, determines significance, makes a decision and issues some directives.
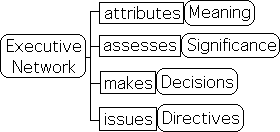
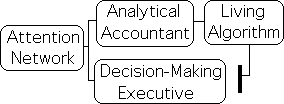
The Attention Network seems to perform multiple functions associated with information. The first 2 networks seem to automatically filter and analyze sensory information and then pass on relevant results to the Executive Network. The relationship is similar to that between an accountant and an executive. The accountant provides the analysis and the executive makes the decisions. Under this perspective, the Attention Network acts as both an accountant and an executive. Attention the accountant is the neurological interface between the flow of sensory information and Attention the executive – our brain’s decision-making center.
The first two networks, i.e. the Alerting and Orienting, seem to perform their analytical accountant functions relatively automatically. We scan our environment, notice something unusual and then focus our attention upon it. This seemingly ‘natural’ process seems to be out of our control. For instance, we turn immediately to attend to sudden loud sounds. In contrast to this mechanical behavior, the Executive Network seems to require time for conscious deliberation and choosing between alternative choices of action.
How does Attention Network perform the accountant’s analytic functions? How does Attention’s focus shift from general to specific and then back again? Are these mechanisms purely biomechanical or bio-chemical? Or could they have a mathematical component? Is it possible that Attention employs a mathematical tool to interpret sensory information streams? Could the Living Algorithm be this mathematical interface? How could the deceptively simple LA assist the Attention Network perform its complicated analytical functions? How is it possible that a mathematical system of any variety could incorporate the possibility of choice implied by the Executive’s decision-making capabilities?
To answer this last question, let us look a little deeper at the innate requirements of Posner’s Attention Model.
Attention Network requires Data Streams to accommodate Choice
Attention in its analytical accountant capacity seems to be an interface between our decision-making executive capacity and the flow of sensory information from the environment. What form does the information take?
According to the well-established Posner Model, the Human Attention Network first monitors the situation and then, if necessary, makes adjustments to a dynamic environment. Due to these features, we will refer to this as the monitor-adjust process. For the monitor-adjust process to occur, it seems that there must be some time increment, no matter how small, between the initial monitoring phase and the final adjustment phase. On the most basic level, the Executive Network requires time to evaluate meaning, make a decision, and then send out directives.

For this reason, we suggest that sensory information comes in pulses, rather than continuously. In other words, the information comes as a discretized stream of data. If the information came in a continuous form, there would be no time to monitor the information, evaluate its significance and then make an adjustment. The trio of networks that make up Posner’s Attention Model requires discrete bits of time between the pulses of info to execute the decision-making process. In order to accommodate the monitor-adjust process, the Attention Network must experience sensory information flow as a discretized data stream.

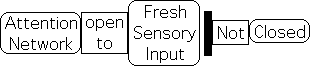
Besides experiencing sensory flows as data streams, the Attention Network must be open to fresh information in order to make timely and appropriate adjustments. Due to the urgent demands of the moment, Attention requires a sense of immediacy in our relationship with sensory information. The transition from the Alerting to the Orienting Network must be relatively instantaneous to be effective, as we must respond as quickly as possible to fresh stimuli.
In this regard, the most recent information triggers the response (the adjustments), not past data. Recent sensory data is most significant, as it reveals what is happening, rather than what has happened. Although not as significant, past sensory data is also important and must be taken into account.
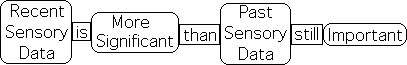
To respond rapidly and effectively to changing environmental demands, current data should be weighted more heavily than past data. This weighting of sensory input from recent to past enables us to adjust more effectively to a dynamic environment.

In addition to being weighted, the data stream moments are also connected. They are related in the sense of context. For instance, is the sensory input growing or fading? How quickly is it growing? The incoming information is interconnected.
![]()
Living Algorithm: Open, Immediate, Interconnected & Possibility of Choice
Let us suppose that the Attention Network employs a mathematical tool to evaluate the constant flow of sensory information from our environment. Let us further suppose that the Living Algorithm is that tool. Is the Living Algorithm capable of fulfilling Attention’s decision-making requirements?
In order to accommodate the monitor-adjust process, the mathematical tool must have the capacity to operate upon discretized data streams. Due to the immediate demands of the moment, the tool must be open, rather than closed, to fresh information. The computational process of Attention’s mathematical tool should also weight recent sensory input as more significant than past input, while still taking prior information into account.
The Living Algorithm specialty is digesting data streams. It is also open to regular environmental input. With each repetition/iteration, of the LA’s mathematical process, a new pulse of fresh information enters the system.
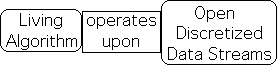
Between each input, there is time for analysis, decision-making, and sending out directives. For example, if our data stream consists of our daily weight, then we have time between each reading to evaluate the data and then decide if we need to reduce, increase or maintain our food intake. In other words between each iteration, there is 'wiggle-room' to evaluate recent input and decide upon a course of action. Due its discretized and open nature, the Living Algorithm is ideally suited to provide the mathematical substrate for the monitor-adjust scenario implied by Posner’s Attention Model.
Further the computational process automatically scales down the impact of past measures. In this fashion, the current data is weighted most heavily in terms of significance and past information is taken into account.

Finally, the Living Algorithm's computational process incorporates past sensory input into the current data stream derivatives. The process that generates these measures provides an interconnectivity between the elements of the sensory input.
Predictive Descriptors, Dynamic Context & Essential Content
It seems that the Living Algorithm is at least the type of equation that can accommodate the Attention Network’s needs for openness, immediacy, interconnectivity and decision-making. How about its computational abilities? Are its mathematical talents able to satisfy the analytical needs of the Attention Network?
Evaluating sensory information flows seems to be a primary function of the Attention Network. The evaluation process enables Attention to both filter out normal and random information and provide a more in depth analysis of unusual information to our decision-making center – the Executive Network. Let us examine how the Living Algorithm’s computational process could assist Attention to perform its analytical functions.
The Living Algorithm specializes in digesting data streams. The computational process provides the ongoing derivatives of any data stream. These measures, i.e. the ongoing derivatives, reveal the ongoing dynamic context of the data stream, i.e. the trajectories of each moment. Due to these capabilities, the Living Algorithm has been deemed the Mathematics of the Moment.
If Attention employed the Living Algorithm as a mathematical interface, it would be able to benefit from the LA's ongoing Predictive Cloud, a trio of measures that describe the position, range and recent tendencies, i.e. the dynamic context of the current moment. Knowledge of the moment’s dynamic context also provides a rough approximation regarding future behavior. In such a way, the Living Algorithm's derivatives could act as predictive descriptors.
Although the Predictive Cloud only supplies rough approximations, the Executive Network could easily employ the data stream measures in a similar fashion to weather prediction. These rough, yet current, approximations of future behavior are far better than nothing. In similar fashion, although the predictions provided by weather networks are frequently wrong, most of us attend the info, as it is also frequently right. The immediacy of the future approximations provided by these ongoing data stream derivatives would be incredibly useful to our decision-making center in a dynamic environment. Although rough, this immediate analysis of a data stream’s dynamic context could facilitate both survival and actualization potentialities.

In addition to the data stream’s dynamic context, the Living Algorithm could also pass on the data stream’s essential content to the Executive Network. The acceleration of erratic or random data streams is flat. In contrast, the acceleration of a data stream with stable content describes a Pulse. This Pulse contains the data stream’s essence. When the Attention Network experiences a Pulse, the data stream’s content could be transmitted to the Executive to facilitate decision-making.
An awareness of both the dynamic context and the essential content of a sensory data stream would enable our decision-making center to better evaluate the data stream’s significance, its meaning. It is certainly useful to know data stream’s identity, for instance whether it represents our mother or a car. It is equally important to have knowledge of the data stream’s dynamic context, whether the data stream’s content is coming or going, how fast it is approaching and its recent tendencies. The Living Algorithm supplies both the dynamics and the essence of a data stream.
Our Executive Network could employ these dual measures to determine the meaning of a sensory data stream. Understanding meaning would enable our Inner Executive to better assess significance and make better decisions. These informed choices could in turn enable us to better fulfill our potentials.
Random Filter, Correlations & Focus Regulation
In addition to analyzing sensory input, Attention could also employ the LA's measures to filter out random data streams. This process would significantly reduce the amount of information that must be sifted through to find some meaningful data streams. This vital function could be achieved by simply attending to data stream acceleration, one of the measures of the Predictive Cloud. Organized data streams exhibit sustained acceleration that rises above certain innate thresholds, while the acceleration of random data streams hovers around zero.
![]()
There is yet another useful feature of this mathematical system. Through basic arithmetic functions, the measures of the Predictive Cloud can also be employed to compute ongoing correlations between 2 data streams (deemed the Living Correlation).
![]()
Note this correlation is ongoing, not definitive. Because of the ongoing nature of this measure, it determines the dynamic, not permanent, relationship between simultaneous data streams.
![]()
Our Inner Executive could utilize the easily computed Living Correlation to determine the nature of data stream relationships. By attending to the results of interactions between data streams, we could take advantage of environmental conditions. For instance, if our ancestors noticed that animals regularly showed up at the waterhole at sunrise, they could utilize this positive correlation to put dinner on the table.
This knowledge could also provide an indication as to how successful a response is to a stimulus. In other words, these ongoing correlations could be employed to distinguish between successful and unsuccessful behavioral strategies. These capabilities could certainly assist us to make better decisions that would assist our quest to fulfill potentials. This understanding is also the foundation of positive and negative reinforcement to regulate behavior.
In Posner’s Model, the focus of Attention seems to shift from general in the Intrinsic Awareness Phase to specific in the Alertness Phase. Unusual information, i.e. a stimulus, seems to trigger this shift. Further once an adjustment is made to the perceived stimuli, Attention’s focus shifts back to general again. In order to effectively evaluate the significance of sensory data streams, it seems that Attention’s focus shifts from general to specific and then back again. Could there be a mathematical mechanism that regulates the focus of Attention?
The Decay Factor is one of the LA’s mathematical features. Due to the ongoing nature of the LA’s measures, they approximate curves. The Decay Factor’s size determines the level of the LA’s ‘focus’. When the Decay Factor is relatively low, the derivatives are more volatile. The contours have greater definition, i.e. the curves are shapelier. Conversely when the Decay Factor is relatively high, the results are more sedentary. The curves are flat with much less shape.
In the resting state (Intrinsic Awareness), the Decay Factor would be set on high – the sedentary range – to better identify dramatic changes. Once a stimulus is identified, a biochemical response such as hormones could automatically turn the Decay Factor down into the volatile range to better analyze the details of the sensory data stream (Alertness Phase). In this way, the Attention Network could readily employ the LA’s Decay Factor to regulate the focus of Attention.
![]()
Let us summarize the computational reasons why the Attention Network could employ the Living Algorithm as a mathematical interface with environmental information. This simple algorithm computes ongoing data stream derivatives that provide the dynamic context for each moment. As predictive descriptors, they provide invaluable information about the present as well as approximations regarding future behavior. The data stream derivatives could also be employed to identify essential content. Knowledge of a sensory data stream’s dynamics and essence would certainly be invaluable information for our Inner Executive.
The same measures could easily, almost automatically, be employed to filter out random streams from consideration, thereby reducing information overload. Further by applying a simple arithmetic process to the data stream derivatives, ongoing correlations between data streams could easily be computed that would facilitate a basic understanding of dynamic relationships. This measure would also provide an indication of the success of our behavioral strategies. Finally, the LA’s Decay Factor could be employed to regulate Attention’s focus.
Although the Living Algorithm can fulfill many of the Attention Network’s computational requirements, there are some significant ones that it can’t fulfill. These functions are associated with the Executive Network. This network must attribute meaning, make decisions and issue directives.
As an automatic mathematical tool, the Living Algorithm is able to provide analysis and even pass on relevant information. However it is unable to assess meaning or make decisions. In similar fashion, the accountant analyzes data and then passes on the knowledge to the chief executive to evaluate the significance and make decisions. Under our suppositions, the Attention Network employs the Living Algorithm as an accountant to perform the analysis of sensory data streams. With this knowledge, our Inner Executive determines meaning, assesses significance, makes choices, and then issues directives.
Simple Arithmetic Computations & Minimal Memory Requirements
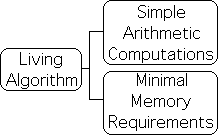
Besides fulfilling the Attention’s aforementioned requirements, the Living Algorithm has other advantages as well. It is easy to compute and the memory requirements are relatively minimal – features that would certainly streamline the analytical functions of the Attention Network.
The computations only require basic arithmetic operations, i.e. addition, subtraction, and division. Cognitive scientists have established that our innate neural networks have the capability to perform these operations. In contrast, the integrals of calculus and the square roots of probability are far beyond our innate computational abilities. While unable to perform the complex computations of calculus and probability, our neural networks can perform the necessary computations required by the Living Algorithm. Our theory is at least possible on a computational level.
Due to the algorithm's mathematical process, the memory requirements are also relatively minimal. The LA's computational process blends the current data with the previous derivative to obtain the current derivative. The entire string of data is not stored, just the most recent measure/derivative. As it could act as a predictive descriptor, this measure could also be emotionally charged, hence easier to remember.
From pragmatic necessity, the Attention Network requires a mathematical system that is both easy to compute and has minimal memory requirements. Straightforward computations based upon small amounts of memory could certainly quicken crucial response time. It is evident that the Living Algorithm fulfills both of these requirements.
Inherent Limitations of Traditional Mathematical Systems
The Living Algorithm seems to fulfill many of the proposed requirements for a mathematical interface between Attention and the Environment. It is open to the flow of environmental information. Easy to compute and with minimal memory requirements, the iterative process provides the 'wiggle room' that is necessary to 'monitor and adjust' to a changing environment. Finally its computational process supplies the dynamic context for each moment. Knowledge of dynamic context could assist the Attention in its executive role to determine significance, i.e. meaning.
While the LA is able to fulfill many of the computational needs of the Attention Network, traditional mathematical approaches2 have some inherent limitations that prevent them from fulfilling the role of Attention’s mathematical interface.
Traditional functions obey the laws of traditional set theory, while recursive functions such as the Living Algorithm do not always obey these laws. Set-based equations have a fundamental regularity that recursive equations lack. Because of their absolute regularity and adherence to set theory, the scientific community has embraced traditional ‘obedient’ functions. Due to their irregularity and lack of adherence, scientists have tended to ignore, even shun, ‘disobedient’ functions.
The obedient functions of science as epitomized by the equations of calculus do a nearly perfect job of characterizing, thereby predicting, the behavior of obedient matter. Due to this perfect match, many scientists hope (have faith) that this type of equation can eventually be applied to human behavior. It is possible that human behavior could be subject to the deterministic nature of obedient equations. However as we shall see, the traditional functions that apply so well, perhaps perfectly, to material systems fall short as a mathematical interface for Human Attention.
While the Living Algorithm is discretized and open, obedient set-based functions are continuous and closed to fresh environmental information. These innate features enable traditional equations to perfectly characterize the automatic and instantaneous reactions of matter that is at the heart of the stimulus-response model. Due to these same features, this mathematical approach is unable address the intentional ‘monitor-adjust’ process that seems to be a significant feature of the Attention Network.

Because of the continuous nature of obedient functions, there is no time to monitor and adjust – no 'wiggle room'. Because they are closed, there is no possibility of fresh input from the environment. Because they describe permanent relationships, the initial conditions determine the outcome. Recent data is unimportant because all results are predetermined. As such, obedient functions don’t provide the sense of immediacy that our Attention Network requires.
Obedient functions do a nearly perfect job of characterizing the behavior of obedient matter – witness modern technology. However, it seems that their innate features prevent them from being Attention’s interface with sensory information. Is it possible that living systems are too unpredictable to be tied down by obedient functions? Could it be that disobedient functions are more appropriate for characterizing the behavior of disobedient Life?

Although traditional functions seem to be inadequate for the task, is it possible that the equations of traditional Probability could be Attention’s mathematical tool?
Probability does a fabulous job of analyzing data sets, but totally ignores data streams, the province of the Attention Network.
![]()
Probabilistic measures characterize the permanent features of a static data set, not the ongoing dynamic context of the data stream's current moment. Probabilistic measures also provide permanent correlations between fixed data sets, instead of providing the up-to-date dynamic measures that our Attention Network requires to make immediate and timely decisions. As the measures of Probability don't address the moment, they are unable to fulfill the immediacy requirement.
In addition, the memory requirements of Probability are enormous, as the entire stream of data must be stored to make the computations. The computations are also exceedingly difficult (requiring square roots). In contrast, only the most recent (emotionally charged) measure must be 'remembered' to make the simple arithmetic computations of the LA’s mathematical system.
Due to the complexity of the operations and the enormous memory requirements, it could be said that only scientists and their students can utilize probabilistic functions to analyze data sets. Attention’s neural networks would have an exceedingly difficult time performing probabilistic functions 'in their head'. In contrast, due to the simplicity of the operations and the small memory requirements, the Attention Network could easily employ the Living Algorithm's measures to obtain relevant information regarding the flow of environmental information, i.e. data streams.
Is information theory of modern electronics a worthy candidate for Attention’s mathematical interface?
Traditional information theory deliberately strips information of meaning. It transforms all forms of information into an impersonal binary form, just 1s and 0s – pure content. Nothing ever touches, but instead remains forever isolated.
This theory, which has enabled and ensured the accuracy of electronic transmission, also destroys information's temporal context. However the Attention Network requires meaning in order to ‘monitor’ and then ‘adjust’ to a dynamic environment. Meaning is based upon dynamic context - the relationship between what is happening and what has happened. Because the mathematics of traditional information theory addresses content, not context, it is unable to convey meaning – a crucial feature of the Attention’s Executive Network.
![]()
In fact, we humans must supply the dynamic context to the perfectly replicated, yet isolated, 1's and 0's in order to appreciate the music, movies, or text contained on our computers or CDs. Could the Living Algorithm provide the mathematical process by which information is transformed into meaning?
Despite their amazing sophistication, the traditional mathematical approaches that we examined have innate limitations that prevent them from fulfilling the requirements of our Attention Network - a sense of immediacy, meaning, and the ability to monitor and adjust. Because they lack certain features, they are unable to supply the mathematics behind our immediate and dynamic relationship with environmental information. As such, the Attention Network could not employ their services as a mathematical interface with the environment.
Could the Living Algorithm be Attention’s tool? As an iterative function that is open to environmental information, it incorporates the monitor-adjust possibility of the Attention Network. Easy to compute and with minimal memory requirements, the LA's Predictive Cloud consists of ongoing predictive descriptors that indicate the dynamic context of the moment - the basis of immediacy and meaning. They could also act as random filters and provide ongoing correlations between data streams. Finally, the Attention Network could employ the LA’s Decay Factor to shift from general to specific and back again. Not only is it plausible, the Living Algorithm seems to be ideally suited to be Attention’s mathematical interface with sensory information from the environment.
The following table summarizes how the Living Algorithm could fulfill the computational needs of the Attention Network.
Attention Network |
Living Algorithm |
|---|---|
Monitor-adjust Possibility |
√ |
Open to Fresh Information |
√ |
Weighting Current Data more than Past Data |
√ |
Connecting Past Sensory Input with Current Input |
√ |
Dynamic Context |
√ |
Essential Content |
√ |
Random Filter |
√ |
Correlations between Data Streams |
√ |
Focus Regulation |
√ |
Simple Computations |
√ |
Minimal Memory Requirements |
√ |
In summary, there is empirical evidence connecting Attention with the LA's mathematical processes. To make sense of this strange connection, we hypothesized that the Living Algorithm could be Attention’s tool, i.e. our mathematical interface with the sensory information. The current article illustrates that it is at least plausible that the Living Algorithm could fulfill this function.
Footnote
1 The article – Mathematics of the Moment – explores the many unique features of the Living Algorithm's system.
2 Check out the article – Contrasts with Traditional Mathematics – for some fundamental differences between the LA's system and traditional mathematical approaches.