Section Headings
- Introduction
- Life’s Computational Requirements
- The Living Algorithm’s Innate Features
- LA’s Averaging Process: Describing Current Conditions
- Predictive Cloud: Ongoing, Up-to-date Descriptive Predictors
- Dynamic Meaning through Layering
- Focusing Attention via the LA’s Leveling
- Random Filter, Thresholds, & Ongoing Correlations
- The LA as Life’s Computational Interface?
Synopsis
This article provides an introduction to the Living Algorithm's many capabilities.
According to our Theory of Attention, Living Systems employ the Living Algorithm (LA) as a computational interface to provide dynamic meaning to the information contained in data streams. What is the justification for this bold statement? The LA has many talents that Life would find appealing.
The LA embodies functional simplicity, as it is easy to compute and has minimal memory requirements. The LA’s repetitive procedure could be described as an averaging, a layering or a leveling. The averaging process provides ongoing measures that would be extremely useful to living systems as descriptors and predictors. The layering process could generate a sense of time by incorporating the past into the present. Providing a temporal context is a necessary component of meaning making. Finally, the LA’s leveling process could be employed to focus Attention.
That is not all. The LA could also provide other useful features as well. Living systems could use the LA’s analytics to filter random data streams, set thresholds, and provide ongoing correlations between multiple data streams. Having these abilities would save mental energy, streamline operations and enhance the decision-making process.
It is evident that the LA could provide a multitude of useful features to living systems. If Life doesn’t employ the LA as a computational interface with environmental data streams, it should.
Introduction
The laws of the physical universe are written in the language of mathematics. We suspect that the same holds true for the living universe. The Mathematics of Matter reveals permanent relationships between a multitude of variables, e.g. temperature, energy and force. Does Living Behavior follow the same laws as Material Behavior? Or are there qualitative differences between the two?
Is the living capacity for Choice the confounding variable that highlights the differences between the mathematics of Life and Matter? Can Life’s decision-making process attain the high degree of predictive certainty expected from the invariable mathematical laws of Matter? Or are contextual probabilities the best predictions that can be expected from a living mathematics? Could it be that a different type of mathematics will illuminate a unique type of mystery regarding living systems?
Life’s Computational Requirements
According to our suppositions, Life and Matter have differing relationships with Information. Exclusively material systems have an action-reaction relationship with Information that does not include Choice. In contrast, living systems employ Information to monitor and then adjust to environmental circumstances.
Due to these differences, Life and Matter have a very different relationship to mathematics. While obeying the invariable laws of mathematics, Matter does not utilize this symbolic language in any other way. In contrast, we hypothesize that living systems actually employ mathematics in their decision-making process. Simply put, mathematics only describes material behavior, while living systems actually utilize mathematics to transform environmental data into a useful form.
What would be some of the minimum requirements for this mathematical tool?
Here is a small sampling of the features that living systems might find useful and even necessary. 1) To minimize mistakes and maximize speed, the tool must be simple to use and have minimal memory requirements. 2) To be sensitive to a dynamic environment, the computational process must be open to new data. 3) In order to incorporate the urgency of the moment, the process must also weight current data more heavily than past data. 4) In order to effectively recognize patterns, it must be able to integrate previous data with current data. 5) To enable choice, the tool must provide ‘time’ for living systems to both monitor and then adjust to environmental conditions. 6) Living systems, of course, require a tool that is able to transform environmental data into a useable form, i.e. meaningful Information. Life has other mathematical requirements, as we shall see, but this will get us started.
Is it possible that a single mathematical tool could fulfill all of these requirements? Could the Living Algorithm (LA) be that tool? If so, what does the LA’s computational process consist of? How does this process fulfill Life’s needs regarding Information? Does the LA provide a powerful mathematical language for living systems?
The Living Algorithm’s Innate Features
LA: Equation
Let us take this opportunity to examine the Living Algorithm in all her naked glory. In order to clarify the mathematics, the simplest version of the algorithm is shown below. Seeing is believing.
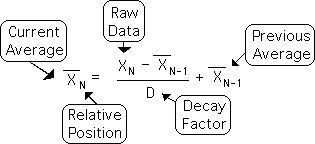
The equation above describes how living systems might effectively digest1. an ongoing data stream. The N subscript in the above equation indicates the relative position of the data point in its respective data stream. The N also indicates that the LA is a repetitive process. With each repetition (iteration) of the LA’s computational process, New Data (XN) is integrated with the Previous Average (Bar XN-1) to produce a new Current Average (Bar XN).
The process has three steps: 1) Find the difference between the New Data and the Previous Average, noting whether it is positive or negative. 2) Divide this difference by a constant, the Decay Factor. 3) Add this quantity to the Previous Average to obtain the Current Average.
This process is not as mysterious and esoteric as it might seem. Each and everyone of us utilizes this simple procedure to assess the probabilities of the surrounding world countless times each and every day from the moment we were born. Humans probably utilize this recipe when engaged in many types of activities, for instance driving a car, walking, cooking, talking and even reading a book. Because of the almost miraculous connectivity of our neural networks, humans are able to exploit a greater percentage of the enormous potentials of this computational process than any other creature. In subsequent chapters, we will examine these claims in greater detail.
Functional Simplicity
Let us examine some of the LA’s innate features that Life might find appealing.
Functional Simplicity
When making immediate decisions, Life doesn’t have the time or capacity for complicated formulas, averaging large lists, square roots or the integrals of calculus. Living systems require computational simplicity for speed and to minimize mistakes. It doesn’t need a rifle to kill a mosquito.
Upon a casual inspection of the above equation, it is evident that the LA only employs simple arithmetic operations, i.e. addition, subtraction, and division. As such, it is fairly easy to compute. The LA’s functional simplicity is ideal for living systems.
Minimal Memory
Minimal Memory Requirements
In order to simplify storage and reduce the chance of error, Life’s computational system would benefit from minimal memory requirements. In the equation above, the LA only requires the memory of one number. This one number is the Current Average, which immediately becomes the Previous Average, when New Data is introduced. Since it is immediately incorporated into the Current Average, the New Data can be conveniently ‘forgotten’. There is no need to ‘remember’ lists of sheer data.
In contrast, it requires long lists of numbers to compute even the simplest average. A baseball player’s ongoing batting average provides a pertinent example. To calculate a player’s batting average, we must add up every hit for the entire season to date and divide it by the number of at bats.
This computational process is very cumbersome. First, a large amount of data must be remembered. Second, the data must be counted, summed up, and divided to obtain an average. Both the computational and memory requirements are daunting for a human without a computer, calculator or even a piece of paper. How about a single Cell or any other living organism with a sense of immediacy? The LA’s computational process and memory requirements are simple in comparison.
Open for Immediacy
Open to external information
Living systems must have a sense of urgency in that they must respond in a timely fashion to dynamic environment conditions. Delay could be fatal, for instance when driving a car. Due this immediacy, Life’s monitoring process requires sensitivity to fresh information. The computational process must have a way of incorporating new data into its system. Of necessity, it can’t be closed to the external world.
With each repetition (iteration) of the LA’s computational process, new data is incorporated into the mathematical system. Because it is open to external information, the LA is called an open equation. The LA’s open nature encompasses immediacy. It is evident that the LA fulfills Life’s openness requirement.
Weighting
Weighting current data greater than past data
Our decision-making process is frequently based upon what has just happened, not on the events of the distant past. We regularly weight the most recent information higher than what went before. Life’s computational process must reflect this data weighting.
The LA’s equation includes D, the Decay Factor. As the name suggests. D represents a rate of decay. With each iteration (repetition) of the mathematical process, the influence of past data upon the current average decays at a steady rate. Put another way, the current average continues to reference past data, but at a declining rate. In such a manner, current data is weighted more heavily than past data. This feature certainly satisfies the weighting needs of living systems.
Discretized Data Streams
Discretized Data Streams to accommodate Choice
In order to monitor and then adjust to environmental information, Life requires time for evaluation, deliberation and decision-making. Data streams are the LA’s specialty. If our suppositions are accurate, information comes in the form of data streams.
The concept of a data stream has some significant implications. The word ‘stream’ implies that Information is not contained in a circumscribed stagnant pool, but rather is an ongoing flow, with new water taking the place of the old. Rather than a continuous flow, the word ‘data’ implies that Information comes in chunks.
Why is this important? Living systems are not food processors, where everything is blended together. Instead information must come in bite-size chunks (data) to render it more easily digestable. This discretization gives Living Systems time to digest the individual pieces of data. Rather than cramming everything in without a break like an engine, bite-size sizes of Information are chewed and then digested before taking in something new. This chunking of information provides Life with time to evaluate, deliberate and make a decision.
LA’s Averaging Process: Describing Current Conditions
It is evident that the LA has many innate features that Life would find desirable, even essential, in a computational process. Now let’s examine what the LA actually does.
Averaging Process
Perhaps the best way to describe the LA’s computational process is as a type of averaging. With each repetition, Raw Data (XN) enters the mathematical system and is immediately assimilated into the Previous Average (Bar XN-1) to generate the Current Average (Bar XN).
LA generates data streams of ongoing dynamic averages
Averages typically determine the middle of a fixed data set. This type of average is also fixed. Rather than fixed data sets, the LA only deals with dynamic data streams, where new data is continually added to the old. Just as the data stream is dynamic, so is the average that the LA computes. Rather than a single fixed average, the LA generates an entire data stream of averages that corresponds with the raw data stream.
Decaying Average & Data Weighting
The LA’s averaging process does not generate a mean or median average, but instead a Decaying Average. The Decaying Average is most akin to a running average. There is however a significant difference. Due to the Decay Factor (D in the above equation), the influence of current data is weighted more heavily than past data. (This nifty feature enables the LA to fulfill one of Life’s computational requirements listed above.)
Due to Weighting, Decaying Ave represents current conditions better than Mean
Just as the mean average represents the middle of a static data set, the Decaying Average represents the middle of a dynamic data stream. While all the data is included in the computational process, the LA’s ongoing average only applies to the most recent data point, not the entire stream. Because the LA consistently weights the present data more heavily than past data, the Decaying Average more accurately represents current conditions than the typical Mean Average.
Batting Average: All data equal weight
Perhaps an example is in order. A baseball player has an annual batting average that is fixed permanently at the end of the season. During the season, he has a running batting average that changes with every at-bat. When computing this running average, every at-bat is weighted the same, from the beginning of the 162-game schedule until the end.
DecAve more accurate on streaks and slumps
In contrast, the LA weights recent at-bats more heavily than distant at-bats when computing the Decaying Average. In such a manner, this averaging process would give a more accurate and up-to-date indication of hitting slumps and streaks. The Decaying Batting Average would be greater than the traditional batting average when the player is streaking and less when the player is slumping.
Life would find useful
Living systems would certainly appreciate an easily computable mathematical measure that provides an ongoing description of current conditions. Life is generally most interested in what is happening right now, rather than what happened in the distant past. In this regard, the LA’s Decaying Average would be very useful.
Predictive Cloud: Ongoing, Up-to-date Descriptive Predictors
Indeed, living systems would be interested in any type of analytic that enabled them to make better predictions regarding future behavior. Making better predictions would certainly assist Life to making better choices in order to fulfill potentials. To incorporate a sense of urgency, these analytics must be ongoing and up-to-date. Further, it would be useful if they could both describe current conditions and predict future behavior. Let’s see what else the LA can do.
LA averaging process applied to Difference between Data and Past
The LA’s averaging process can be applied to any data stream. For instance, it can be applied to the difference in the Decaying Average equation shown above (XN – Bar XN-1). With every repetition (iteration) of the process, the difference between the new data and past average is computed. This ongoing difference also generates a data stream.
Generation of Deviation & Directional Data Streams
When the LA’s averaging process is applied to this data stream of differences, it generates two ongoing averages. If the difference is treated as a sheer magnitude (a scalar), i.e. not positive or negative, then the LA generates a data stream of what we call Deviations. If the positive or negative aspect of the difference between data and average is taken into account, the LA generates a data stream of what we call Directionals.
Location, Range, Tendencies: Predictive Cloud
The Decaying Average indicates the average location of the data stream. The Deviation indicates the data stream’s average range. The Directional indicates the average tendencies of the data stream. The three as a group are called the Predictive Cloud, for reasons we shall see.
Predictive Cloud applied to Hitting Stream
Let’s see how the Predictive Cloud applies to the batting average. When a player’s hitting stream exhibits a relatively large Deviation, this indicates that a player’s batting is erratic, while a small Deviation would indicate stability. A large and positive Directional would indicate that the player’s hitting is just getting hot, while a large and negative Directional would indicate that the player is cooling off.
Past Performance predicts Future Performance
The batting average, which describes the player’s current performance, is also employed by managers and owners to predict future performance. Similarly with these measures. They can both describe the player’s current performance and simultaneously act to predict future performance.
PCloud: Descriptive Predictors
How about an example? Suppose two players have similar batting averages, but different Directionals. According to the stats, the player with a negative Directional would be much less likely to get a hit than the player with a positive Directional. Descriptions can frequently be employed as predictors. This is why we call the LA’s trio of descriptive averages the Predictive Cloud.
Predator could employ Predictive Cloud to capture Prey
The relevant, weighted, and timely information provided by the Predictive Cloud regarding any data stream could certainly be useful to any living system. For instance, a predator could readily employ the trio of measures to assess the probable location, probable range, and probable tendencies of his prey. Having this understanding could certainly increase the probability that he would get fed and thereby survive to pass on his gene pool.
Only 3 Measures need be remembered
Despite the utility of the Information provided by the Predictive Cloud, only 3 values need be ‘remembered’, i.e. stored in memory. The sheer data, i.e. ‘raw’ and differences, can be immediately ‘forgotten’. Even the past averages can be ‘forgotten’. Only the current averages need be ‘remembered’. As they are emotionally charged due to relevance of current conditions, these 3 measures are even more likely to be ‘remembered’.
Dynamic Meaning through Layering
LA’s overlay process provides context that is basis of Meaning
To make appropriate choices, living systems must attribute some kind of Meaning to sensory data streams. For instance, a frog infuses meaning into visual data streams – transforming them into an edible bug, a feared predator, or even a desirable sex partner.
How is meaning generated? How does the LA’s computational technique assist Life to impart Meaning to Raw Data? How is this accomplished?
As well as an averaging, the LA’s technique could be called a layering process. Current data is overlaid upon an accumulation of past data to create averages that describe the current moment. The successive experiences of these layered moments generate a temporal context. A sense of time underlies history and memory. This potential for temporal sense is the foundation of dynamic context. Context is a necessary component of meaning.
The Predictive Cloud provides us with a good example of how Life could employ the LA to impart Meaning to environmental data streams. The three measures that constitute the Predictive Cloud provide useful Information regarding the dynamics of any data stream. Living systems could certainly employ these analytics to better fulfill potentials. In this way, the LA’s computational process transforms raw data streams into ongoing measures that could prove useful in our quest for self-actualization, e.g. survival.
What is the nature of the Meaning that these analytics provide?
The Predictive Cloud conveys Information regarding the dynamic features of any data stream. We’ve suggested that the PC’s three measures indicate the average location, range, and tendencies of the data stream’s current moment. These ongoing averages are in a constant state of flux. Another way of conceptualizing these measures is as the data stream’s velocity and acceleration. They indicate rates of change, not fixed conditions.
The Predictive Cloud does not convey information regarding the static features of our environment, e.g. color, shape or even feeling. However, it could describe the dynamic features of these qualities. Rather than a photograph, the LA’s derivative measures could be more likened to a movie. The Meaning derives from movement and context, rather than sheer content.
The LA’s logic derives from our relationship to sound, rather than sight. This is an important distinction. The logic derived from sight is set and content-based. For instance in a stationary snapshot, the relationships and content are permanent. Generally speaking, the objects in a picture are well-delineated. It is either in the set or it isn’t.
In contrast, the logic of sound is dynamic, contextual, and continually decaying. For example when we listen to a piece of music, the notes are continually fading unless they are deliberately sustained. There is no permanence. Although we can experience the same recording over and over again, the individual sounds come into existence for a brief time and then are immediately replaced by new notes. However our hearing process overlays the current notes upon the past notes to impart the context that is necessary to actually experience the music.
Focusing Attention via the LA’s Leveling
Focusing Attention
Most Living Systems, if not all, require a method for focusing Attention. When in a relaxed state of alertness, we attend to general environmental features. If an event captures our attention, i.e. stands out from general trends, we shift our focus from general to specific environmental details. How is this shift of focus accomplished?
As well as an averaging or layering, the LA could also be called a leveling process. Extreme data points, whether ‘raw’ data or differences, are immediately assimilated into the average. In this fashion, the computational process ‘levels’ (smoothes) the data stream’s potentially erratic curve and replaces it with a more stable and moderate curve of ‘averages’.
The LA’s Decay Factor, D in the above equation, determines the stability and moderation of this curve. When D’s value is small, e.g. 2, the averages are more extreme and less stable. When D’s value is large, e.g. 20, the averages flatten out and become very stable.
If an organism could somehow regulate the Decay Factor’s size, it could employ the LA’s leveling process as a tool to focus Attention. For instance, if D is small, details are heightened. Conversely, when D is large, the data stream’s broad outlines are emphasized. By regulating D, the organism could easily shift Attention from the general to the specific features of the data stream and back again. In such a manner, Life could employ the LA to regulate focus.
Random Filter, Thresholds, & Ongoing Correlations
The Living Algorithm has many other features that Life could utilize to both save precious energy and optimize the decision-making process.
Random Filter
Living systems from the cellular level on up could employ the LA’s measures to differentiate random from meaningful data streams. By attending to specific measures, Life could employ the LA to filter random data streams from consideration. This automatic process could save an substantial amount of mental energy.
Setting thresholds
Living systems could readily employ the Predictive Cloud to set thresholds and then reset them as circumstances demand. For instance, Deviations, which indicate probable range, could determine an acceptable range or threshold. Over time, these mathematical thresholds could become biological, hence more binding and less variable. In turn, living systems could employ the Decaying Average to determine when the threshold is approached or crossed.
Interactive Probabilities: Component of Pattern Recognition
Ongoing Correlations: Interactive Probabilities
The LA could also provide ongoing correlations between 2 data streams. By ‘remembering’ just a few of the LA’s ongoing analytics, life forms could easily determine if 2 data streams are moving in tandem, in opposition, or have no relationship. This knowledge would enable organisms to make elementary causal connections. This type of pattern recognition would certainly assist the decision-making process.
Just as the Predictive Cloud acts as a both descriptor and a predictor, these ongoing correlations both describe the current relationship between 2 data streams and predict future behavior. The LA’s relatively simple arithmetic techniques could enable living systems to compare data streams to determine interactive probabilities, which could be used in predictive capacity.
In contrast to the LA’s computational simplicity, it generally takes a college course in Probability and Statistics to learn how to generate a correlation between 2 sets of data. Currently, the confusing computational process is normally performed by a computer. Previously, the student had to use tedious tables to compute square roots and look up correlations
Does anyone really believe that Cells, or even humans for that matter, memorize complicated formulas in order to calculate probabilities and correlations? Wouldn’t living systems instead prefer ongoing probabilities and correlations that require little memory and only arithmetic operations to compute?
The LA as Life’s Computational Interface?
Our suppositions suggest that living systems have a computational relationship with environmental data streams. It is evident that the LA has many features that Life would find appealing.
Logic: LA Functional simplicity & Useful measures
The LA embodies functional simplicity, as it is easy to compute and has minimal memory requirements. The LA’s repetitive procedure could be described as an averaging, a layering or a leveling. The averaging process provides ongoing measures that would be extremely useful to living systems as descriptors and predictors. The layering process could generate a sense of time by incorporating the past into the present. Providing a temporal context is a necessary component of meaning making. Finally, the LA’s leveling process could be employed to focus Attention.
That is not all. The LA could also provide other useful features as well. Living systems could use the LA’s analytics to filter random data streams, set thresholds, and provide ongoing correlations between multiple data streams. Having these abilities would save mental energy, streamline operations and enhance the decision-making process.
It is evident that the LA could provide a multitude of useful features to living systems. If Life doesn’t employ the LA as a computational interface with environmental data streams, it should.
Footnote
1. The LA’s sole function is to ‘digest’ data streams. We deliberately employ the word ‘digest’ rather than ‘process’. Just as the stomach’s digestion process converts raw material into a form that is valuable to the organism, the LA’s digestion process transforms Raw Data into meaningful Information.