Mathematics of Attention? Only Life has the ability to focus attention, not Matter. We've all heard of mathematics applied to material systems. Uncountable equations exhibit the relationships between energy, force, speed, mass and myriad other variables. But who has heard of a mathematics of living systems, much less a mathematics of attention, experience, information and knowledge?
What if the mathematics of Life is of a fundamentally different nature than the mathematics of Matter? What if living systems require reflexive equations to emulate their inherently reflexive nature? However because they contain themselves, reflexive equations aren't included in the family of material equations that dominate the sciences. Equations that refer back to themselves, as do living systems, are excluded because they don't necessarily obey the laws of traditional set logic. Could these reflexive equations that are open to the possibility of informed choice obey their own kind of laws and perhaps even have a different type of answer? Will these answers yield testable predictions?
This article suggests answers to these questions and much more. It begins by proposing a mathematics of living systems based upon a single reflexive algorithm digests information in an iterative fashion. After examining the differences between material and reflexive functions, an equation is developed that relates Attention, Experience, Information and Knowledge. Finally, we explore the testable predictions of the Attention Formula.
Section Headings
- A. Living Algorithm's Derivatives: Living Average & Directional
- Reflexive Living Algorithm Equations: Disobedient & Open
- Ongoing Number Strings & Pulse Strings
- Pulse Strings: Specific Number of Identical Elements
- Processes are Answers to Living Algorithm's Number String Equations
- B. A Brief Example of the Computational Process
- C. Startling Answers of Living Algorithm's Number String System
- D. The Algebra of Attention, Experience & Information/Knowledge
- E. Attention Formula: Testable Predictions
A. Living Algorithm's Derivatives: Living Average & Directional
Previous writings have established multiple patterns of correspondence between living behavior and Attention in the mathematical system of Information Dynamics. The Living Algorithm generates this system by digesting data streams. This digestion process reveals the dynamics of each moment in the data stream. The following article explores the mathematics of Attention from the perspective of the Living Algorithm.
A1. In the article Divided Attention & Information Dynamics, we 'derived' the following equation. The expression links Attention, Information, and Experience with the Living Algorithm. Let's examine and refine the algebraic details to better understand the nuances of the process.
![]()
A2. We begin with the Information Digestion process. It is based in the Living Algorithm. The Living Algorithm generates a set of equations that compute all the rates of change, i.e. derivatives, of a data stream. Further these derivatives are ongoing, characterizing the dynamics of each moment. Following is the equation for the 1st derivative, the velocity of the data stream. Because the 1st derivative is also the data stream's ongoing average, it is called the Living Average.
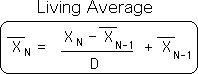
A3. Following is the equation for the 2nd derivative, the directed acceleration of a data stream. Deemed the Directional, it is written in the same format as the Living Average (data stream velocity) to exhibit that it is based upon the same algorithm. There are also many higher Directionals. Because of its primacy as the first, we frequently refer to it as the Directional. (Note: Data streams also have a non-directed acceleration, deemed the Deviation.)
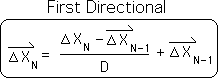
A4. Let us write the equation in a format that is more convenient for our purposes. Following is the definitional formula for ∆XN.
![]()
A5. Substituting this expression into Equation 3 yields the following result. This is an algebraic representation of the Information Digestion process referred to in Equation A1.
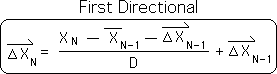
A6. Following are the elements of the equation. A new data point XN enters the system with each repetition, i.e. iteration, of the mathematical process. The Previous Living Average and the Previous Directional must be retained in order to compute the Current Directional. The Decay Factor, D, is a fixed constant that determines the rate of decay.

Reflexive Living Algorithm Equations: Disobedient & Open
7. To understand the significance of these elements, let us speak briefly about the class of equations generated by the Living Algorithm. These equations have several features that set them apart from standard equations. First they are reflexive/self referential, a.k.a. recursive functions. In other words, each of the Living Algorithm's equations contains itself in the sense that it refers back to itself with each repetition, i.e. iteration, of the mathematical process. For instance in Equation 6, the Current Directional (indicated by the N subscript) is a function of the Previous Directional and the Previous Living Average (the N-1 subscripts). Similarly in Equation A2, the Current Living Average is based upon the Previous Living Average.
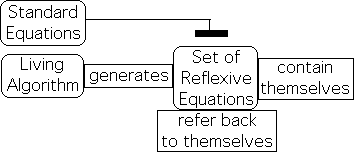
8. Because each equation contains itself, traditional set logic does not apply to these equations. This means that the equations generated by the Living Algorithm do not obey the same rules that apply to the standard type of equation that dominate contemporary science. For instance, the sophisticated approximation techniques of standard mathematics don't necessarily apply to reflexive equations. This is why the Living Algorithm's offspring are deemed disobedient equations. Mandelbrot's fractals are also generated by a recursive function, i.e. a disobedient equation.
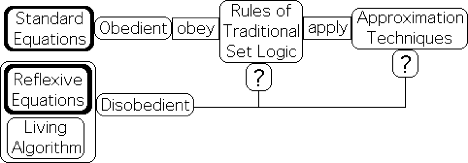
9. There is a second feature that sets the Living Algorithm's mathematical system apart from the standard mathematics that is the foundation of hard science. The algorithm's equations operate on data streams. The N subscript indicates the position in the data stream. With each iteration (repetition) of the mathematical process, a new data point (XN) enters the Living Algorithm system. This means that this class of equation is open in the sense that new information enters the system with each repetition of the mathematical process. This openness enables the possibility of choice.
10. This openness is not true of every reflexive equation. For instance, Mandelbrot's fractal equation is not open to the outside world. Standard Equations are also closed. For both the standard equations of Physics and Mandelbrot's equation, initial conditions are set and everything follows in a deterministic fashion. Because the Living Algorithm is both open and disobedient, it encompasses the possibility of choice.
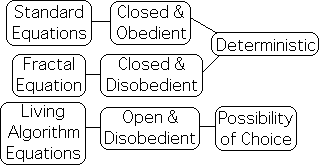
11. With both traditional equations and Mandelbrot's equation, there is only one answer. In contrast, the Living Algorithm generates a data stream of answers that corresponds with the data stream that it digests. In fact, a cloud of answers surrounds each data point. These reveal the dynamics of each moment. In this discussion, we are only interested in one of these derivative data streams - the data stream of acceleration.
Ongoing Number Strings & Pulse Strings
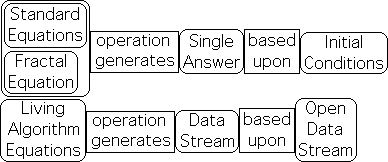
12. Each of the Living Algorithm's equations generates a data stream of derivatives. The Directional computes the 2nd derivative, i.e. the acceleration, of a data stream. In other words, the Directional transforms one data stream of numbers into another data stream of numbers. The 2nd data stream indicates the ongoing acceleration from moment to moment.
13. Mathematically, these numerical data streams can take 2 basic forms. The numbers in the data stream can change or they can remain the same. For our purposes, those data streams with identical elements, deemed Number Strings, are far more significant. In fact, the mathematics of Attention is primarily based around Number Strings. In contrast, data sets with identical elements are of virtually no interest in traditional set theory.
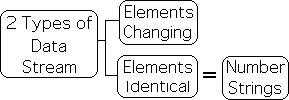
14. Just as there are 2 types of numerical data streams, there are also 2 types of Number Strings. There are ongoing Number Strings and Number Strings with a specific length. The second are most significant in terms of Attention. For reasons that we will discuss, these are deemed Pulse Number Strings, or just Pulse Strings for brevity.
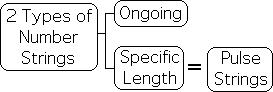
Pulse Strings: Specific Number of Identical Elements
15. Why are data streams with a specific number of identical elements so significant to the Living Algorithm system that they require their own name? Let's examine what happens when the Living Average digests a Number String consisting solely of Ks. Following is a visual representation of the process.
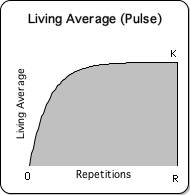
Notice that the Living Average starts at 0 and then rises to K. Mathematically, the Living Average approaches K as long as new Ks enter the system. Pragmatically it reaches K after a specific number of iterations/repetitions of the Directional process. We will call this number R for repetition.
16. Now let's examine what happens when the Directional digests a Number String consisting solely of Ks. Following is a visual representation of the process. Because of its striking appearance, we have deemed this mathematical process the Pulse.
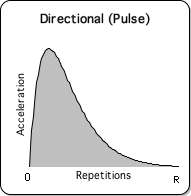
Notice that the Directional starts at 0, rises to a peak, and then falls back to 0. After attaining the peak, the Directional approaches 0 as long as new Ks enter the system. Pragmatically, it reaches 0 after a limited number of iterations/repetitions of the Directional process. It takes the Directional the same number of repetitions, R, to reach 0, as it takes for the Living Average to reach K. Based upon 2 factors, the number of repetitions, R, is somewhat discretionary. Although discretionary, the range is small and finite.
17. We define a Pulse Number String to be a data stream consisting of R identical elements. The pulse-like appearance of the Directional graph combined with its importance inspired the name of this highly significant type of Number String. We employ the following circle notation to denote a Pulse String consisting of Cs. C is greater than 0.
![]()
For brevity, we also refer to the Pulse Number String of Cs, as a Pulse of Cs. Reiterating for retention, this means that the data stream consists of R elements called C.
18. If C = 1, then the following is true. This is a Pulse of 1s.
![]()
19. Now let us factor the C out of the Pulse String (Equation 17). Because of the disobedient nature of the equation, we were required to prove that this operation was valid. (For the proof, see Number String Proofs.) This yields the following result. C times the '1' Pulse String.
![]()
20. This factoring process does not apply to a Pulse of 0s, as it remains the same. The Pulse of 0s is unique and separate from the Pulse of 1s. For reasons that will be discussed, the Pulse of 1s will be also called the 'On' Pulse and the Pulse of 0s will also be called the 'Off' Pulse. Recall that each of these Number Strings has R elements – the number required to generate a complete Pulse.
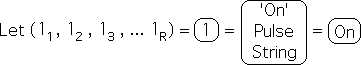
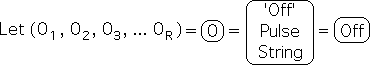
21. Due to the fact that the essence of all Number Strings are 'On' and 'Off' Pulses, which consist solely of 1's and 0's, the content of the Living Algorithm's Number String System is essentially binary.
Processes are Answers to Living Algorithm's Number String Equations
22. Just as with many other features of the Living Algorithm Pulse System, the answers are of a different nature than those in Standard Equations. In brief, the answers in this system represent an entire process, i.e. a Pulse. In contrast, Standard Equations and Mandelbrot's Fractal Equation yield a specific result. Let us take Einstein's famous equation, E = mc2, as an example. Once we know the initial conditions, mass in this case, we can compute the amount of energy.
23. The Living Algorithm certainly yields individual results. In fact, the Predictive Cloud consists of a series of individual results that may be employed to make rough predictions regarding the future behavior of prey, predator or mate. In this case, the Living Algorithm digests a changeable/variable data stream, instead of a Number String. The numbers in the data stream represent/symbolize some type of environmental condition, perhaps location. If the numbers symbolize location, the answers would be probable location, probable range, and probable tendencies at each moment.
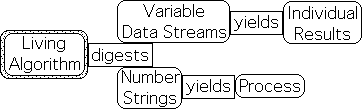
24. However, when the Directional digests a Number String, it yields a process, not an individual number. When the Living Algorithm digests a Number String, specific results are relatively meaningless. As mentioned when the Living Average digests a data stream consisting of As, the answer approaches A.
![]()
Similarly when the First Directional or any other Directional digests this same data stream, the answer always approaches 0.
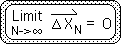
Because these results are almost intuitive, they reveal little in terms of new information.
25. However, if we look at the answer as a process rather than as a single event, the results are startling to say the least. The unexpected results arise due to the reflexive nature of the equation. Because of the lack of parallels within standard mathematics, the Living Algorithm process demands a new type of notation.
26. When the Directional digests On and Off Pulses in a variety of combinations, the only meaningful result is a process. After the initial conditions are set, i.e. the nature of the Pulse String, the answers to the equation are a process. This essentially binary system yields 3 basic processes.
1) a Positive Pulse: the basic ideal Pulse that we have been discussing
2) a Negative Pulse: the inverse of the Positive Pulse
3) No Pulse: a Flat Line
27. We will employ the following notation to indicate these processes.
![]()
![]()
![]()
28. Reiterating for retention, the Directional digests a finite Number String to yield a data stream of results, i.e. the Number String's acceleration. The individual answers are of no interest. The entire data stream is what draws and holds our attention. Because our answer is an entire process rather than a single result, we were 'forced' to employ this novel notation.
B. A Brief Example of the Computational Process
Recall that the Directional digests an entire data stream to reveal a process. This process is the answer. For clarity, let us examine what happens when the Directional digests the simplest Number String, i.e. a data stream composed of exactly R 1's, a.k.a. the 'On' Pulse. Let's start at the beginning, i.e. with the 1st individual result of the entire process.
B1. Following is the operational equation for the 1st Directional, (Equation A5 above).
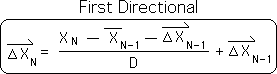
B2. N, the position of the first data point equals 1 by definition. XN, the 1st data point of the data stream, also equals 1 by definition, as there are only 1s in the data stream. Substituting these values in the above equation yields the following result.
![]()
B3. Because the computational system is based upon what went before, we must fix these numbers. To allow the system to start from rest, we let the initial Living Average and the initial Directional equal 0. This is known as 'Zeroing out the System'.

B4. D, the Decay Factor, can be any positive number. For ease of computation, we let D equal 10.
![]()
B5. Employing these values in Equation B2 yields the following value for the first point in our process.
![]()
B6. Substituting the appropriate values into the Living Average formula (Equation A2) yield the following answer.
![]()
B7. Let us now compute the 2nd data point (N=2) in the process. Substituting 2 for N into the Directional formula (Equation B1) yields the following equation.
![]()
B8. X2 equals 1 by definition, as all the Xs equal 1 in the On Pulse. We substitute the values from Equations B4, B5 and B6 into the equation and then perform the computation. This yields the following answer for the 2nd data point.
![]()
B9. If we repeat the process R times, the Rth Directional approaches 0, as mentioned above.
![]()
B10. Simultaneously, the Rth Living Average approaches 1.
![]()
B11. If we graphed each of the elements in the process the result would be the Pulse. Because R, the number of iterations, is normally greater than 100, a computer spreadsheet is required to perform the necessary computations. Only 3 columns are necessary: 1) the Data, 2) the Living Average, and 3) the Directional.
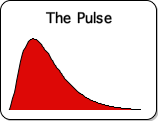
The above sequence constitutes the mathematical process when the Directional digests a Pulse of 1s, i.e. the 'On' Pulse. The answer is a process, the Pulse. We showed the mathematics for illustration only.
B12. Let us now write this entire mathematical process in a less cumbersome manner – in a fashion that highlights the significance of the answers. There are symbols for the processes of summation, integration, and differentiation. However, there are no mathematical symbols for the mathematical processes of the Living Algorithm, including the Directional. Let us introduce a simplified notation to indicate this procedure.
B13. We will indicate the entire computational process with the symbol '§'. The '§' operator transforms an entire data stream into another data stream via the Directional. The transformed data stream reveals a process. (In contrast, the summation operator '∑' adds up a specified string of numbers to yield a single numerical result.)

B14. As an example, when the Directional operator § digests the On Pulse String, it generates a Positive Pulse.
![]()
The above equation represents the entire computational process that was illustrated in this section.
C. Startling Answers of Living Algorithm's Number String System
Now that we have established some algebraic foundations for the Living Algorithm's Number String System, we are ready to examine the surprising, even startling, answers. Let us explore some of the unique mathematical features of this essentially binary system.
C1. Let us start with the most basic transformation, just mentioned. When the Directional digests a data stream composed entirely of 1s with a length of R, i.e. the 'On' Strings, the result is the Ideal Pulse, i.e. the Positive Pulse.
![]()
C2. When Directional operates on the 'Off' String, the result is a flat line, the '0' Pulse, as might be expected.
![]()
C3. Recall that a Number String consists of identical elements by definition. Because of this convenient fact, the Content can be factored out, which leaves the Pulse of 1s, a.k.a. the 'On' Pulse. Let C represent this Content.
![]()
C4. This is the result when the Directional operator digests this type of data stream. C acts as multiplier or even modifier. If C is larger than 1, the Positive Pulse is amplified. If C is between 0 and 1, the dimensions of the Positive Pulse are diminished. If C is not a number, it reveals the content of the Positive Pulse. In each case, the shape of the Pulse remains the same.
![]()
C5. So far, no surprises. Let's see what happens when we combine some of these Pulse Strings. First a notational definition.
![]()
C6. When the Directional Operator digests 2 consecutive 'On' Strings, the result is not 2 Positive Pulses, as might be expected. Instead the answer is a Positive and Zero Pulse.
![]()
This result is unheard of with Standard 'content-based' Equations. Relationships between variables are fixed and permanent, forever and ever. Two plus two always equals four. Gas and electrical laws don't change because of a changing context. However, our 'disobedient' Directional Equation is 'context-based'. By itself, an On String generates a Positive Pulse, but when the context changes, the result changes. When an On String follows an On String, the result is instead the Zero Pulse.
C7. In similar fashion, when an Off String is isolated, it generates a Zero Pulse. But when an Off String follows an On String, it generates a Negative Pulse. With a change in context, the Off String yields an entirely different answer when digested by the Directional.
![]()
C8. When an On String follows an On String, the result is the Zero Pulse. However, when it follows an Off String, it generates a Positive Pulse. Context, not content, determines the result with these reflexive equations. This is one way in which reflexive equations are disobedient.
![]()
The unusual features of this contextual mathematical system go on and on. For instance, 'interruptions' in the Pulse Strings yield interesting results. When the contextual behavior of the other data stream derivatives is also taken into account, the Living Algorithm system is vast.
D. The Algebra of Attention, Experience & Information/Knowledge
D1. The prior analysis is pure mathematics. Let us examine how the Living Algorithm's Pulse System links up with Attention, Experience and Information/Knowledge. We begin with Equation C4, an unadulterated numerical relationship.
![]()
D2. We hypothesize that the 'On' Number String of 1s corresponds with the Conscious state, when Attention is 'on'. Alternately, the 'Off' Number String of 0s corresponds with state of Sleep, when Attention is 'off'. As we shall see, a multitude of scientific 'facts' have provided validation for this hypothesis.
D3. Assuming that this relationship is true, a single bit of Attention would correspond with the '1' that is digested by the Directional in the 'On' state. Let A stand for this single bit of Attention.
![]()
D4. In this case, a single A would equal 1 or the On state.
![]()
D5. If the 1s of the On String symbolize Attention, then a Pulse of 1s would symbolize uninterrupted Attention. By extension, the On String would correspond with Sustained Attention.
![]()
D6. Substituting this algebraic expression for Attention into Equation C4 yields the following result.
![]()
D7. Recall that the On String generates a Positive Pulse when digested by the Directional. We hypothesize that the Positive Pulse is associated with a completed, or integrated, Experience. Experience is defined any event that leaves a permanent memory trace, i.e. changes our neural networks. This includes a wide range of possibilities, anything from a sensory experience, to a lecture or movie. Let E symbolize a bit of Experience, i.e. a single step in the integration process.
![]()
D8. If E symbolizes a bit of Experience, then we hypothesize that the Positive Pulse is associated with an Integrated Experience.
![]()
D9. Substituting the above expression into Equation D9 yields the following equation.
![]()
D10. All we have left are the Cs. Recall that C represents the Content of the Pulse String. Recall that Pulse Strings consist of R identical elements. If the Pulse String consists of 5s, then C equals 5. If the Pulse String consists of a face, then C equals a face. If the Pulse String consists of anger, then C equals anger. As these examples illustrate, the content, C, of the Pulse String is not restricted to numbers. To differentiate the purely mathematical formula from the experiential formula, let us call the first C of the equation, I, the Information contained in the Pulse String.
![]()
D11. Recall from D7 that an Experience is defined as a change in the neural networks, for instance memory consolidation. Further Equation D9 associates Experience with a completed Pulse. As such the second C in the equation is associated with information that is integrated into our cognitive system. In other words, the pure information, I, of the Pulse String has been transformed into what we will call knowledge, which we will denote with a K.
![]()
D12. Following is the complete Attention Formula.

D13. Let us verbalize the formula. When Attention is sustained upon Information for a sufficient duration, it generates a completed Pulse of Experience, whereby the Information contained in the Pulse String is transformed into Knowledge, i.e. a change in the neural networks. Further, the Directional's information digestion algorithm drives this entire process. In brief, the Attention Formula is a mathematical process that exhibits the requirements for how inert Information is transformed into useable Knowledge in living systems. Due to its similarities with biological digestion, we refer to this process as information digestion.
D14. Let us summarize the relationships. Attention is associated with the Pulse of 1s, i.e. the On Pulse. As such, it consists of discrete bits, 1s. Experience is associated with the Pulse generated by the Pulse String of 1s. As such, it consists of slivers of varying lengths, all of which are substantially less than 1. Information is associated with the Content of the String, i.e, the focus of Attention. Information can be numerical or non-numerical, such as a face. Knowledge is associated with the Information that is transmitted to the neural networks via the information digestion process. It takes a complete Experience Pulse to accomplish this task.
E. Attention Formula: Testable Predictions
As might be imagined, there are many testable predictions associated with the formula for Attention. Let us offer a brief sampling.
E1. On the most fundamental level, the equation is based upon the underlying assumption that Attention is linked with the Directional's digestion process. Due to the iterative nature of the digestion process, the implication is that Attention is 'quantized' rather than continuous.
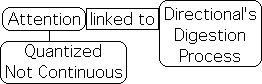
Recent research into brain waves indicates that this prediction is probably true. Quoting from a recent New York Times article (May 2015), Dr. Gregory Hickok, a prominent researcher in the field, writes:
"The brain samples the world in rhythmic pulses, perhaps even discrete time chunks, much like the individual frames of a movie. From the brain's perspective, experience is not continuous but quantized."
Our equation predicts that the quantized nature of Experience is due to our method of information digestion – the Living Algorithm.
E2. One of the prime benefits of equations is that they reveal relationships between variables. The Attention Formula states clearly that Attention must be sustained for sufficient duration to have an Experience, i.e. neural networks are changed. If this is true, then the reverse is also true. If Attention shifts too rapidly from topic to topic, then humans won't experience, i.e. integrate the information.
Cognitive science provides validation for this prediction. Multiple experiments have firmly established that sustained Attention is required for memory consolidation – the basis of critical thinking. Memory consolidation and a Life-changing Experience are identical in that they both transform information into knowledge that reconfigures our neural networks. (See the article on Shifting Attention.)
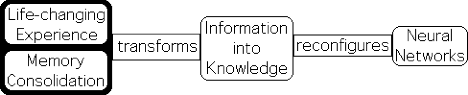
Likewise, interruptions to Attention can mar an ideal Experience, whether it is a productive session, a movie, or even sex. (See the article on Interruptions.) The Attention Formula predicts that these phenomena are due to the manner in which humans digest information.
E3. The Attention Formula (Equation D12) is the foundation equation of Information Dynamics, just as Newton's expression for force, F = ma, is the foundation equation of Physics. Many other equations are derived from these foundation equations that reveal significant relationships that also make testable predictions. Let's examine some of the fundamental implications of Equation C6, shown below.
![]()
E4. First, let's write the equation in terms of the variables of the Attention Formula. Employing the appropriate notation of Attention and Experience yields the following expression.
![]()
Briefly, the equation states that the first Pulse of Attention generates a Pulse of Experience, while the second Pulse of Attention generates zeros, i.e. nothing. The implication is clear. Attention can't be sustained on a single topic forever or it flat lines. As the digestion process only yields 0s, no information is transformed into knowledge; no more neural networks are changed. If the assumptions behind the Attention Formula are valid, then the above equation predicts that humans, as living systems, should have a distinct attention span for a single topic. Cognitive science's 10-minute rule provides validation for this prediction.
E5. If Attention is likened to the Conscious State, the equation predicts that we can't remain awake forever, because we cease to digest information after a certain point. The digestion process only generates 0s, not a life-changing experience. This prediction is certainly validated on a daily basis. It is a well-established fact that humans must sleep or their system shuts down. Indeed, humans can go longer without food and water than without slumber. The scientific community has no explanation for the omni-present Sleep Necessity Phenomenon. The Attention Formula suggests that it has to do with the way we digest information.
E6. So how is Attention refreshed, if it can't be sustained forever? For plausible answers, let's look at another Attention equation: Equation C8 from above.
![]()
Following is a visualization of the result.
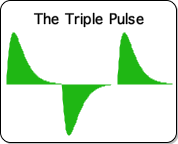
E7. As is evident from the title, this is the famous Triple Pulse. We have written a series of articles on the many patterns of correspondence between the Triple Pulse and living behavior, especially regarding sleep-related activities.
![]()
E8. What does this equation predict? For clarity, let us substitute the appropriate equivalences. The On Pulse of 1s is when Attention is 'on', i.e. the Conscious State.
![]()
E9. The Off Pulse of 0s is when Attention is 'off', i.e. the Sleep State.
![]()
E10. Substituting the above notation into Equation E6 yields the following result.
![]()
E11. The implication of the equation is straightforward. Consciousness must alternate with Sleep to maximize our potential for Experience. Without slumber, Attention flat lines, as in Equation E3. With an appropriate Pulse of Sleep, Attention is refreshed and with it the ability to experience the world. We have all experienced the refreshing nature of sleep.
E12. The cognitive community has firmly established the converse. Experimental evidence has firmly established that Sleep Interruptions have a negative impact upon our cognitive abilities the following day. In parallel fashion, when interruptions (1's) are introduced into the Off String (0s) in the Triple Pulse sequence, the dimensions of the final Positive Pulse are reduced, even though its content and the method of digestion remain the same.
E13. Let us illustrate the mathematics with some simplified notation. Let the numbers after the Directional (the left side of the equation) indicate a series of Pulse Strings. Let the numbers after the equal sign (the right side) indicate a series of Pulse Types.
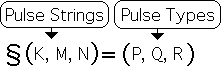
E14. Following is the exact numerical equivalent of Equations E6 and E11.
![]()
E15. We indicate an interrupted Pulse of 0s with 0.1. When the Pulse of 0s is interrupted, the ideal potentials of the last two Pulse Types are diminished. Even though the Directional digests an uninterrupted Pulse of 1s the second time around, it can only generate an '0.8', (a diminished Pulse) rather than a '1' (the ideal Pulse). In other words, the mathematics of the Triple Pulse mimics scientific results regarding Sleep Deprivation and our cognitive abilities, which certainly seem to be related to our capacity for Attention.
![]()
This is just a small sampling of the testable predictions associated with the Attention Formula and the derivative equations. Indeed the patterns of correspondence between Information Dynamics and empirical reality are multiplying. Thus far, there has been no contradictory evidence. Could there be a confounding variable that has not been taken into account? Is it possible that random fluctuations account for the similarities between living systems and this mathematical system? Or could it be that living systems actually digest information via the Living Algorithm? Is that why Life seems to be subject to the innate patterns of information digestion?
Will intense professional scrutiny, and more specific testing of the predictions reveal that these theories have no more substance than the summer fog? Or will time and additional experimentation show that the underlying assumptions of Information Dynamics are rock solid?
For more on this topic, check out the next article in the series – the Theory of Attention.