Section Headings
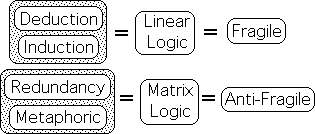
- Fragile Linear Logic vs. Anti-Fragile Matrix Logic
- Matter’s Deduction & Induction vs. Life’s Metaphoric & Redundancy Logic
- Astronomy Example of Metaphoric Logic’s Anti-Fragility
- Scientific Realism vs. Instrumentalism & Human Conflation
- Matrix Logic Emerges from Linear Logic
Fragile Linear Logic vs. Anti-Fragile Matrix Logic
(√ 1.9 pgs)
Is Logic Dependable? Proves motion and choice don’t exist
After exposing his personality flaws, you might wonder if Logic can be counted on to be a trustworthy companion. After all, he hangs out with impossible characters like imaginary numbers and infinitesimals. Further he can prove by logical necessity that motion and choice don’t exist – certainly absurd notions for most of us – at least those who haven’t been deluded by reason.
Logic one of my best friends despite not entirely dependable
Yet Logic remains one of my best friends. Despite his internal contradictions, I frequently rely upon his advice in many matters, even though he is not always completely dependable. Actually at times, he is even a bit erratic and misguided.
Teasing Deduction, who is part of Logic Family
But I have unfairly maligned my friend. Rather than unitary, as implied, Logic is the family name for a group of related Logics. I was mainly teasing Deductive Logic and those who worship him blindly – his logical impossibilities notwithstanding. Although indispensable for the language of mathematics from whence he derives his prestige, Deduction is part of a larger family.
Ideally: Family Counsel for collective conclusions
Ideally, the family members consult with each other before drawing a cooperative conclusion. As a group, there results are very dependable. Virtually all human beings regularly rely upon their collaborative efforts to navigate our uncertain world.
Super-logical forget other family members
Unfortunately the super-logical regularly forget the other members of the clan in their obsession with Deduction. He is the rigid family member that draws necessary conclusions from unchallengeable assumptions. Perhaps the intellectuals prefer him because of his absolute rigor.
Deduction acting alone can derive outrageous conclusions
Despite, or perhaps because of, this rigor, Deduction sometimes draws some supposedly ‘necessary’, yet outrageous conclusions. They even verge at times on the unbelievable – probably due to misguided or unrefined assumptions. That is frequently the problem when he goes it on his own.
Family collaboration to cross check results
Sometimes he is so full of himself that he ignores contradictory evidence – the elephant in the room. I just smile tolerantly and try to reign in his excesses by consulting with the other family members. I keep hoping that he might listen to their balanced and stable counsel. He really needs to collaborate with his family – cross-check his results to examine if they are reasonable.
Proud Deduction, not a good listener
This is not as easy as it might sound. More than a little proud of his achievements, Deduction is not a good listener. He is actually quite passionate about his inferences – even inspiring humans to write books in favor of these reasonable, but sometimes unverified conclusions. Occasionally, he has no supporting empirical data whatsoever; incontrovertible facts even contradict his supposed necessary ‘truths’.
Deduction, while a Star, needs other family members to keep him on track
Don’t get me wrong. For certain tasks, Deductive Logic is the only one for the job. Can’t do without him. He is a definite star. Yet there is a big but. He needs his other family members to keep him on track. Isn’t that what friends are for – to give us feedback on our resolutions and conclusions?
Why? Linear Deduction & Induction are fragile – good for tightly defined problems
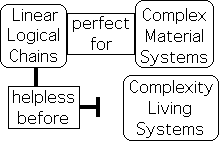
Why does he go astray? Deduction and his constant companion Induction are linear in nature. Linear logic is fragile because it is only as strong as the weakest link. Like an arrow or spear, linear logic is perfect when the target is precise. They are great at solving tightly defined problems – when assumptions and facts are incontrovertible – when cause and effect are identifiable.
Linear Deduction perfect for complex Matter Systems
Material systems, even if they are very complex, have this feature. For instance, their distinct components can be precisely quantified. For this reason, Deduction’s linear logic is the perfect tool to deal with Matter.
Linear Logic inept at analyzing the complexity of Living Systems
However complex and complexity are orders of magnitude apart in difficulty. Atomistic material systems are complex, while holistic living systems have complexity. Due in part to the multiplicity of their interactive relationships, holistic systems resist strict definitions. In these situations, Deduction sometimes, maybe even frequently, misses the mark. When wrong, the chain is completely broken. Linear logic is generally inept at analyzing the complexity of Living Systems.
Deduction & Induction get in trouble when left alone with Life
Deduction and his sibling Induction should rarely be left alone, especially when it comes to Life. They’re always getting into trouble – causing no end of mischief with their bizarre conclusions. But we love them for their passionate exuberance. How we love it when Eureka is on their face. They come in beaming. “Look at this amazing idea that we have deduced.”
Direct Experience to damp unreasonable conclusions of Linear Logic
Sometimes we must reluctantly damp their enthusiasm – throwing the cold water of direct experience over this misguided fire. But other times, their discoveries fit perfectly into the logical matrix – making it even stronger than ever. To be honest, it was their work that uncovered and identified the more global members of the Logic Family. Bless them.
Redundancy and Metaphoric: Matrix-based Logic
In contrast to the linearity of Deduction and Induction, two of their relatives are based in multi-dimensional matrices. This self-supporting web of logical chains include Deduction and Induction. Rather than a single chain, these matrices consist of Metaphorical Blends and a Redundancy Network.
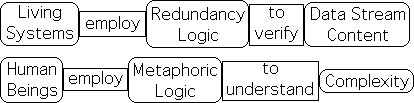
Living Systems employ Redundancy Logic to verify DS Content
Due to the complexity of environmental interactions, all living systems employ Redundancy Logic as their prime form of logic. For instance, sensory redundancy is necessary to correctly identify a data stream’s content. Constantly checking and cross-checking results is essential for survival. In similar fashion, it frequently helps to consult outside sources when making crucial decisions.
Humans employ Metaphoric Logic to understand Complexity
While all living systems use redundancy logic to cross check conclusions, all humans also employ metaphorical blends to better understand the complexity of their world. Metaphorical blends are at the heart of every complex abstraction from philosophy to mathematics to religion to social interactions. This form of logic is also one of the foundations of language. Without metaphorical blends, we would not be humans.
Linear Logic Precise: Matrix Logic General
There is a tradeoff however. When Deduction and Induction join talents to solve the problems associated with atomistic material systems, they are unbeatable. Their solutions are generally as precise as the data associated with quantifiable phenomena. In contrast, the other family members are not quite as precise.
However, Matrix Logic can tackle complexity, while Linear Logic can’t.
Compare linear conclusions with multi-dimensional matrix
What’s the method? How do we utilize the Logic Family’s balanced talents to draw and validate conclusions? Compare the linear conclusions of one half of the family with the multi-dimensional matrix of the other half and then proceed cautiously. If all family members point in the same direction, we march forward confidently. But if there are contra-indications, we might have to restructure the web.
Challenges strengthen anti-fragile Matrix
Yet this challenge rarely unravels or damages the entire network. Stress only makes the matrix stronger. The Logic Family’s collaborative effort creates a logical network that gets ever stronger with each stressor. Unlike the fragility of Linear Chains, a Logical Matrix is anti-fragile – as it benefits, rather than breaks, from stress.
Subsequent Section more in depth analysis
Who are these mysterious members of the Logic Family, those that form a Matrix rather than a single linear chain? The following section exhibits how linear logic is appropriate and sufficient for complex material (non-living) systems, while the complexity of living systems demands a matrix-based logic.
Matter’s Deduction & Induction vs. Life’s Metaphoric & Redundancy Logic
Metaphoric Logic?
Metaphoric and Redundancy Logic? What’s the matter with Deduction and Induction? Why does one pair apply to Matter and the other to Life? And what is the significance? To better understand the meaning and importance of our presumed strangers, let’s examine how they fit into the categories of traditional logic.
Deduction & Induction: antiquated re: Living Systems
We are taught that there are two types of logic: deduction and induction. This traditional division of logic into these specialized parts is a bit antiquated when it comes to Living Systems. While working relatively perfectly with Material Systems, it is a flop when it comes to Life. Due to the interactive feedback loops associated with monitoring and adjusting, living organisms are orders of magnitude more complex than sheer Matter. While the physical is merely complex, the living has innate complexity.

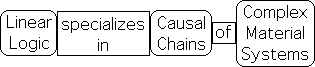
Matter’s simplicity subject to cause-effect: Deduction’s specialty
Due to Matter’s relative simplicity, it is possible to identify causal chains. The Linear Logic of Deduction and Induction specializes in causality. If this happens, then that happens, by necessity. Modern technology is based in the precise causal chains of material systems.
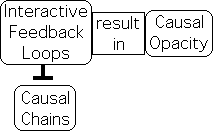
Life’s complexity > Causal Opacity
Life’s far greater ‘feedback-loop’ complexity makes it virtually impossible to identify causal chains. The interactive interconnectivity between subject and object renders cause and effect nearly meaningless, except on the simplest levels. While causality is off limits due to its opacity, it is possible to identify living processes.
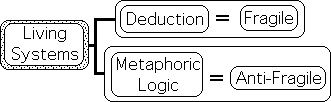
Life requires Stable, as in not fragile, Logic
Due to her complexity, Life requires a type of logic that is stable, as in not fragile. Due to their linearity, the conclusions of Deduction and Induction are quite fragile. One flaw breaks the logical chain.
M&R Logic stable as Matrix-based
Due to their multi-dimensionality, the conclusions of Metaphoric and Redundancy Logic tend to be quite stable due to their anti-fragility. Although a portion of the logical matrix might be compromised or challenged in some fashion, the entire web adjusts and remains. In such a way, Life is able to regularly adjust and refine her model for dealing with the dynamic circumstances of existence. Stressors strengthen rather than weaken the anti-fragile1 Logical Matrix.
Deduction: Assumptions > Necessary Conclusions
Let’s be a little more specific. Deductive reasoning draws necessary conclusions from basic assumptions. Mathematics is based upon deductive reasoning.
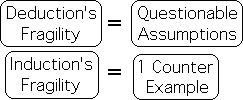
Deduction Fragile: Bad Assumptions > Bad Conclusions
The fragility of this type of reasoning comes from the assumptions. If the assumptions are weak, the conclusions are weak, no matter how impeccable the logic.
Induction: Specific Examples > Generalizations
Inductive reasoning makes generalizations from individual examples. It is a form of pattern recognition. If we get nauseous every time we eat fried food, we infer that fried food makes us nauseous. The logic is linear. Science is based in part upon inductive reasoning. Scientists attempt to generalize the patterns, i.e. find the rules, behind empirical data.
Induction Fragile: 1 counterexample voids hypothesis
This form of reasoning is fraught with peril. No matter how many examples are accumulated, one counter example voids the conclusion. If all the Latinos that we encounter are working as laborers of one kind or another, we might infer that Latinos are poor and uneducated. If we meet one brilliant Latino, we must change our conclusions. This form of reasoning is at the root of racial stereotypes. Due to this factor, Induction is a fragile form of logic that must be employed cautiously.
Metamorphic Logic: From System to System -> More Reliable
While Inductive Logic infers a general pattern from a few individual examples, Metaphoric Logic makes inferences based upon similarities/symmetry between the logical structures of two systems, hence the term matrix. The logic is multi-dimensional rather than linear. Because of this dimensionality, Metaphoric Logic is far more stable and reliable than Induction.
Metamorphic Logic: If 2 systems exhibit logical symmetry, Then can employ known to understand unknown
Rather than individual examples, Metaphoric Logic makes inferences based upon the recognition of multiple logical symmetries between two systems, e.g. mathematical system and empirical data. Once a metaphoric relationship has been established, living systems can employ the logic of the known system, e.g. mathematics, to better understand the unknown system, e.g. a phenomenal network.

Powerful Metaphoric Logic basis of verbal abstraction
Indeed Metaphoric Logic is so powerful that it is the basis of human abstraction. Although unnamed, we have employed this potent and stable form of logic to understand and navigate our dynamic environment. In this sense, this form of logic is not so unfamiliar after all.
Multi-dimensional Redundancy Logic: most stable
The conclusions based upon Redundancy Logic are even more stable as Deductive, Inductive and Metaphoric Logic can all be a part of its multi-dimensional matrix. Redundancy Logic relies upon cross-validation from as many sources as possible. While Deduction and Induction are exceedingly fragile due to their linearity, Redundancy is anti-fragile in the sense that conclusions are strengthened via refinement with each stress upon the system.
Living Systems rely upon Redundancy Logic
While humans in particular rely upon Metaphoric Logic to form abstractions, living systems in general rely upon Redundancy Logic to form a stable conception of their environment. Our five senses provide a great example. Each sense generates a different type of information. Yet we blend these signals to stabilize our understanding.
Redundancy separates dream from reality
We hear rustling and then look to see if there is anything there. We might even detect a certain fragrance that identifies a flower, tree or child. If possible, we reach out to touch the plant or an unexpected friend. These final forms of validation cement the deal. Redundancy Logic separates dream from reality.
Summary of Logical Types
The following statements summarize the four kinds of logic that we have examined. (Note: this list is not exhaustive.)
Deduction: Assumptions -> Necessary Conclusions
Induction: Few Examples -> Generalized Pattern
Metaphoric: Logical Structure -> Logical Structure
Redundancy: Multi-Dimensional Logic -> Stable Conclusions
Linear Logic perfect for causality of Complex Material Systems
Deduction and Induction are perfect and sufficient for complex material systems as they are based in absolute content. Identifiable essence enables definitive assumptions, which in turn lead to definitive conclusions. In such a way, definitive causal chains can be identified.
Linear Logic helpless before Complexity of Living Systems
However, these standard linear forms of logic are relatively helpless when it comes to the complexity of living systems. One layer of complexity: organisms must first evaluate and then respond to an ever-changing environmental context. A second layer: the multiplicity of interactions between multiple components, e.g. the brain’s neural networks, results in causal opacity.
Living Systems employ Matrix Based Logic for stable conclusions
For a deeper form of validation, all living systems employ redundancy logic. Humans add metaphorical blends to the mix. As they are matrix-based, the conclusions of both kinds of logic are far more stable than those based in linear logic. Life’s complexity requires multi-dimensional logical matrices.

Living systems can’t afford to only employ the linear logical chains of Deduction and Induction to draw conclusions. The fragility of the conclusions threatens survival. A faulty assumption and/or a single counter-example can easily be fatal. One flawed decision is all it takes to eliminate that particular gene pool forever.
In contrast, the logical matrix is anti-fragile, as stress makes the network’s conclusions ever stronger. Time regularly tests the inferences of this logic, which results in constant refinements to the system. Unable to depend upon the fragility of linear logic, living systems must instead rely upon the anti-fragility of matrix logic to draw more dependable time-tested conclusions.

Following Chapters exhibit how M&R validate Math-Fact Matrix
Subsequent chapters exhibit how these unusual, yet powerful forms of logic provide validation for the Math-Fact Matrix that defines each Realm of Existence.
Astronomy Example of Metaphoric Logic’s Anti-Fragility
Intro
Anti-Fragility of M&R’s Matrix Logic
Elevating Deduction and Induction over Metaphoric and Redundancy Logic is like mistaking the branches for the tree. While branches can easily break off, the tree remains and actually grows more branches to replace the dead ones. Similarly while the fragile conclusions of linear logic (Deduction and Induction) might be proved wrong, the anti-fragile systems founded in the matrix-based logic of Metaphoric and Redundancy Networks just get stronger by forming new logical branches.
If assumptions ironclad, Deduction = not-fragile
Don’t get me wrong about the linear fragility of Deduction. If the assumptions are ironclad and the reasoning is sound, then the conclusions are indestructible. Tightly defined mathematical proofs are of this variety. The results are true in every time and place forever and ever. Amen.
Mathematical Deduction Indestructible, Living Deduction fragile
In the case of mathematics, the conclusions drawn from Deduction are shatterproof – neither fragile nor anti-fragile – neither breakable nor do they get stronger with stress. They are just true – end of story. However, if there are any questions whatsoever about the assumptions, as with living systems, then Deduction’s linear logic is quite fragile.
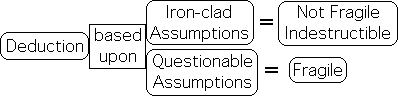
Math/Matter = Perfect Assumptions; Life = Provisional Assumptions
It is possible to make unchallengeable assumptions in both mathematics and material systems. However, due to interactive feedback loops, it is impossible to make these same inviolable assumptions regarding living systems. Assumptions are always provisional in that they are dependent upon a dynamic context, for instance the ubiquitous yet dynamic appetite. The questionable nature of the assumptions result in equally questionable conclusions on the part of Deduction.

Metaphoric Logic = anti-fragile: Article provides AstroExample
In contrast to the fragility of linear logic, matrix-based Metaphoric Logic is anti-fragile, in that every stress on the system makes it stronger. Let me provide a powerful historical example of how Metaphoric Logic was and is employed to understand the Heavens.
Body
Initially: Earthly Existence as metaphor for Heavenly Behavior
In the beginning humans throughout the planet used their earthly existence as a metaphor (conceptual2) to better understand celestial behavior. Generally speaking they anthropomorphized their world. They projected the logic of human existence upon the Material World3.
Successful Strategy: Astrology: Ex. Anti-fragility of Metaphoric Logic
Although not perfect, this strategy must have been relatively successful, as it has persisted for millennia – probably the best option at the time. Gradually, the Mediterranean cultures began anthropomorphizing the planets as gods, e.g. Venus and Mars. They even projected human personality traits on these presumably large material spheres. Astrology is a vibrant vestige of this way of understanding reality and a good example of the anti-fragility of metaphoric logic, for better or worse.
Ancients developed math system to predict & align with Planetary Gods
In the quest to anticipate and thereby align with these planetary gods, ancient astronomers began plotting the positions of the heavenly bodies. With regular exposure to these astronomical data streams, their ‘scientists’ began perceiving regular and predictable patterns. Over many more centuries, they developed a rudimentary mathematical system to better represent these patterns and thereby predict planetary position – the ultimate aim. This strategy began the practice of employing the mathematical metaphor to better understand physical reality – a strategy that is at the heart of science.
Global Cultures employ Math to make astronomical predictions
Cultures all over the world have employed a variety of systems to make astronomical predictions. Presumably for divination or religious purposes, humans have charted and predicted eclipses, equinoxes, solstices, and even lunar cycles with great precision by employing rudimentary mathematical systems. There are many successful examples of this sort throughout the world, e.g. the Stonehenge culture in England and the Anasazi Indians of New Mexico.
Mediterranean: Planets: Culminates with Ptolemaic system
In the ancient Mediterranean cultures, notably those located in Chaldea, Babylon, Egypt and Greece, the predictive ability of the mathematics gradually extended to include planetary position. At the beginning of the Common Era, this cross-cultural collaboration culminated in the Ptolemaic system. Ptolemy developed a sophisticated mathematical system that could provide a good estimate of where a planet might be located in the Zodiac at any time. This freed diviners and priests from having to rely upon erratic nightly observations, as they could now rely upon Ptolemy’s mathematics.
Math/Astronomical Metaphor lasts Centuries. Why? Anti-fragility
This metaphoric relationship between the two systems, mathematical and empirical data, i.e. celestial observations, was so strong that it lasted for a millennia and a half. The facility and relative accuracy of the planetary predictions was a definite factor in the staying power. Another significant factor had to do with the anti-fragility of the metaphoric relationship. Rather than break, the system became stronger from stress.
Constant Refinement due to Stress
The amazing endurance of Ptolemy’s astronomical Math-Matrix was due to constant refinement. Due to stressors on the systems, i.e. inaccurate predictions, Ptolemy’s system was regularly refined over the centuries. Rather than discard the system due to errors, the astronomers of many cultures instead worked to fix it – to make it better, stronger, more able to make accurate planetary predictions further into future. Rather than breaking from stress, the overall system became stronger from stress. Rather than fragile, the metaphoric relationship was anti-fragile.
Stress of more accurate observations
What did the stress consist of? More accurate observations exposed discrepancies in the metaphoric relationship between observation and prediction.

Refinements add complications, rather than simplify
New generations of astronomers gradually resolved these predictive discrepancies by adding refinements, e.g. adding epicycles.
However the refinements that resolved the predictive stress simultaneously generated stress of a new kind. Rather than simplifying, each new resolution simultaneously added a new level of complication. The stress of this increasing complication introduced fragility into the mathematical metaphor. Systems generally thrive on simplicity and fall apart with too many complications. Simpler is better. Less factors to break down. Easier to fix.

Disturbed by Ptolemaic Fragility, Copernicus introduces new conceptual metaphor, Not Math
The fragility (complications) of the Ptolemaic metaphor disturbed Copernicus tremendously. He claimed that God would never create such a cumbersome, unaesthetic and even monstrous arrangement. His disdain for the ancient system inspired him to take another approach – heliocentric rather than geocentric.

While he introduced a new metaphor for understanding astronomical reality, the underlying assumptions of his mathematical system remained the same – perfect circles at a constant velocity.
Copernican system: Different Conceptual Metaphor, Same Math Metaphor as Ptolemy
However, Copernicus’ conceptual metaphor did not really achieve its aims of simplification. Why? Copernicus employed the same mathematical assumptions as Ptolemy (perfect circles at a constant velocity). As the new was fairly equivalent with the old metaphor regarding predictive power, there was no impetus for change. (If it works, don’t fix it.) Accordingly, the heliocentric metaphor just gathered dust as a curiosity for the better part of a century after it was introduced.
Kepler replaces Ptolemaic Mathematical Metaphor: ellipses replace circles
Then came Johannes Kepler. Tycho Brahe developed a more precise way of plotting planetary position. The precision put such stress upon the fragile complications of the Ptolemaic metaphor that it cracked. Rather than merely fix the old system with more complicated refinements, Kepler developed a new mathematical system with new assumptions. Ellipses replaced circles; a changing velocity replaced a constant velocity; and the planets now revolved around the Sun rather the Earth (Copernicus’ only real contribution).
Requires Simpler & Better Predictions of Kepler’s Math Metaphor to replace Ptolemaic metaphor
While Copernicus introduced a new conceptual metaphor, it was really Kepler’s mathematical contribution that ultimately led to the replacement of Ptolemy’s astronomical metaphor (both conceptually and mathematically). Kepler’s new metaphor was both simpler and made better predictions. A win and win.
![]()
Kepler’s Mathematical Metaphor requires refinements: stressors (better data) strengthen anti-fragile network
Despite its advantages, Kepler’s new mathematical metaphor has required tweaking and modifications over the last three centuries to deal with the stress of ever better data. Refinements were introduced to account for the discrepancies between fact and theory. Rather than trivial as in the case of the Ptolemaic system, some of these adjustments led to huge leaps in both mathematical and scientific understanding. The stress inspired the development of new and productive branches of mathematics. The stressors did not break a fragile system, but rather strengthened the anti-fragile metaphoric network.
Math to Phenomenal Network = Anti-Fragile Metaphor
It could be said that applying mathematics to a phenomenal network, in this case celestial behavior, is the meta-metaphor. The anti-fragility of this metaphoric system has been so powerful that the metaphor has lasted for millennia, ever since it was first introduced. The actual math systems regarding astronomy went through only one major revision during all that time. This alteration created a cultural cataclysm – a battle between the Science and Religion that has been ongoing on some level even since.
Science’s prime anti-fragile metaphor, as witnessed by growth from stress
This resistance to change illustrates the incredible staying power, the stability of metaphoric logic due to its anti-fragility. All the stressors, increasingly precise data, generated adjustments that resulted in modern Science. Yet the basic metaphor remains the same: Mathematical logic can be employed to better understand the logic of phenomenal networks.

Example indicates need for Correct Math System: Life requires New math System, not Material Mathematics
However not all types of mathematical logic are the same, as our example clearly illustrates. Kepler’s ellipses about the Sun replaced Ptolemy’s circles about the Earth. In similar fashion, the logic of Material Mathematics, both Molecular and Quantum, does not fit the logic of Living Systems. Instead Living Logic is a better fit with the logic of iterative mathematics, such as DS Dynamics provides. The metaphoric relationship between Life and this Mathematical system is anti-fragile in that stress makes it stronger.
Scientific Realism vs. Instrumentalism & Human Conflation
Requires Battle to replace Strong Ptolemaic Metaphor with New Metaphor
Ptolemy’s traditional metaphor, as mentioned, had become incredibly stable over centuries due to its anti-fragility (becoming stronger from stress). Replacing the old and venerated with a new conceptual metaphor generated a scholastic and cultural furor. First Luther and then the Catholic Church banned the new heliocentric metaphor as an assault on traditional reality – Ptolemy’s geocentric metaphor. Galileo was, of course, a notable victim of this conflagration over replacing the old metaphor of understanding the heavens with a new one. This astronomical example is but one of many examples from the history of science exhibiting the difficulty of replacing an old metaphoric matrix with a new one.
Why is there such a resistance to change in both human culture and the scientific community? We suggest that it concerns our human tendency to conflate metaphor with reality. Rather than acknowledging that the relationship between the internal logic of a mathematical system and the internal logic of a phenomenal network is metaphorical, many brilliant individuals impart reality to the metaphor. They then fight desperately to defend their imagined reality. To see a potential flaw in Conflation, let us apply this reasoning to our Ptolemaic example.
Ancient Astronomy: First to employ Math as Metaphor for Reality
Ancient astronomy provides one of the first instances of matching mathematical logic with the logic of a phenomenal network. Establishing logical symmetries is the first step in Metaphoric Logic. The second and crucial step is employing the known to better understand the unknown.
Ptolemy’s Mathematical Matrix à Celestial Bodies move in Perfect Circles at Constant velocity
In this case, Ptolemy’s mathematics was based upon the assumption that all celestial bodies move in perfect circles at a constant velocity around the Earth. This assumption presumably originated from applying the logic of the Sun, Moon, and fixed stars to the planets. The motion of these primary heavenly bodies was regular and invariable from day to day, season-to-season, year in year out. If the Sun and Moon, why not the planets? Surprisingly, Ptolemy’s system reinforced this metaphoric logic, providing the matrix with a high degree of plausibility.
Scientific Realism vs. Instrumentalism
There are two basic types of intellectual responses to the Ptolemaic system, i.e. his Math-Fact Matrix – scientific realism and instrumentalism.
Sci. Realists: Math is Reality
Scientific realists hold that mathematics represents the underlying structure of reality – the truth beyond superficial appearances. Math is reality. Many great scientists from Aristotle to Einstein have held this perspective.
Instrumentalists: Math a metaphor for Reality
Instrumentalists hold that mathematics provides description rather than explanation. Rather than being reality, mathematics instead provides a precise metaphor for understanding reality. Many great scientists from Ptolemy to Maxwell and Poincare have held this perspective.
Ongoing battle between 2 Perspectives continues
The war continues to rage between the two perspectives. A recent book attributes complete reality to mathematics, considering the rest, including even matter, to be ephemeral. A Buddhist physicist argues the opposite: that mathematics only provides a metaphorical map of reality, but is not reality.
Ptolemy’s Math: Example of Flaw of Scientific Realism
Let us employ the Ptolemaic example to exhibit a potential flaw in scientific realism. The accuracy of the Ptolemaic system in predicting planetary position indicated that all heavenly bodies move in perfect circles at a constant velocity.
Ptolemy & Greeks believed Math an instrument, not reality
Ptolemy himself and many other Greek astronomers did not hold this position. They believed that mathematics described reality, but did not explain it. As a predictive instrument, math is metaphor, not reality.
After conflating Ptolemaic metaphor with reality, ensuing Generations fought to defend imagined reality
It was the ensuing generations that began attributing reality to Ptolemy’s system of planetary prediction. From the Arab civilizations through to Medieval Europe, the educated tended to believe that the planets really moved in an elaborate system of epi-cycles and such. After conflating the metaphor with reality, the Establishment, both scholars and religious authorities, fought desperately and intensely to maintain their position – to defend their imagined reality.
Conflationary Process: Aggressive defense of Territory
The conflationary process inadvertently blinds us to alternate perceptions of reality. Of even more significance, we fight aggressively to protect our assumed territory from foreign invaders. In the process we create boundaries of us and them. Are you for me or against me or better yet against my imagined reality which is me? Further we try to convince others to join our imagined reality, hoping that these followers with assist us in defending our position from real or imagined attacks.
Conflation a common human tendency as conserves mental energy
Conflating metaphorical understanding with reality is a common human tendency. The simplification associated with conflation transforms subtle and contextual nuances into either right or wrong. While conserving mental energy, this tendency can also be misleading, as in the case of the Ptolemaic system. Believing the metaphor to be real obscures inconsistencies.
Mathematical Metaphor never perfect fit, always discrepancies
Just as with any metaphor, mathematics is never a perfect fit. Conflating mathematics with reality results in ignoring or minimizing, e.g. treating as anomalies, the discrepancies between fact and theory. Metaphorical understanding is based in the notion that that there will always be irresolvable discrepancies hiding in the corners.
May Gods protect me from Conflation – Fat Chance
May the gods prevent me from conflating my own mathematical metaphor with living reality. Hah! Fat chance. I am human after all. Guarding against is the best I can expect.
Matrix Logic Emerges from Linear Logic
(√ 1.8 pgs)
To say that Matrix-based Logic is a special form of Linear Logic is like saying that a plane is special form of a line. While consisting of an infinite number of lines, a plane is much more than a line. A plane has an extra dimension.
It could even be said that a plane is an emergent feature of lines, i.e. not foreseeable from knowledge of the constituent parts alone. In other words, the features of the Collective (plane) are unpredictable from the Individual parts (lines). Planes are the unexpected, even somewhat magical, result of placing an infinite number of infinitely thin lines together. Surprise of surprises. This infinite summation yields an extra dimension – from a one-dimensional line to a two-dimensional plane.
In the same way, it could be said that Matrix Logic (Metaphoric Systems and Redundancy Networks) is an emergent feature of Linear Logic (Deduction and Induction). Matrix Logic definitely has special unimaginable characteristics that can’t be derived from the constituent parts. For instance, while Linear Logic is fragile, Matrix Logic is anti-fragile. The first can break from a little stress, while the second gets stronger from stress, within certain limits of course.
This dichotomy between logics illustrates another difference between Life and Matter. Matter merely reacts to the laws of Linear Logic. In contrast, Life must actually employ Matrix Logic to survive. These multi-dimensional logical networks are stable enough to grow and provide effective strategies for survival.
Due to the anti-fragility of Matrix Logic, the longer the matrix has persisted, the longer it will continue to persist. Roughly speaking, a matrix’s age is a good predictor of how long the system will continue to survive. This is very different from living systems with their limited life span or fragile objects, which can break at any moment.
Classics provide a good example. The longer they have been around, the longer they will be around. Homer’s Iliad & Odyssey have been around for over 2 millennia, which indicates that they will probably be around for at least another few millennia. By contrast, there are no guarantees with pop culture. A novel that is a best seller today might only last another year in publication. However, once a book has endured 10 years, it is likely that it will last another 10 years.
A new book, e.g. a mystery, can break (lose appeal) from the stress of even newer books with similar content and themes. Classics survive because they have some special indefinable ingredient that sets them apart – makes them worth rereading over and over again in different times and places.
The same analysis holds for Matrix Logic. Time inherently generates punctuated stresses. As anti-fragile systems, each stressor makes the logical matrix stronger. As the matrix gets stronger, this simultaneously increases the longevity of the metaphoric system or redundancy network.

Re Evolution and Redundancy: the longer a Redundancy Network has lasted, the longer it will probably last. This property of anti-fragility explains why evolutionary logic is so stable. A few millennia is one level of persistence, as in the case of classic literature, but a few hundred million years, as in the case of biological systems, is another matter altogether. Our many senses provide the best example of an integrated Redundancy Network that is not going away.
Re Metaphoric Systems: This type of logical system is primarily, if not exclusively, human, as it is wedded to words and language. The longer a Metaphoric System has endured, the longer it will endure.
The monistic Metaphoric Systems related to Matter and the Biblical God have been around for millennia. Monism is not going away any time soon. The resistance to replacing these anti-fragile systems is incredibly strong.
However, they do have an Achilles heel – a point of fragility – their inability to address a huge phenomenal network related to Attention. Just hoping to sneak in through these cracks.
Sometimes stress can break even a long term matrix. This was true, as we saw, in the case of Ptolemaic system. The stress of a new simplified system that makes better predictions finally undermined the complicated fragility of the old metaphor. There are no guarantees – just tendencies.
While my Math-Fact Matrix only exists in my finite mind, I believe that its anti-fragility will allow it to last forever (if it ever gets an audience). Although less likely with each passing year, black swans do exist.
Footnotes
1 I employ the term antifragile, as coined by Nassim Taleb in his book of the same name Antifragile. An antifragile system is one that becomes stronger from stress, as opposed to fragile systems which break from stress.
2 As mentioned ad nauseum throughout this work, Neural Linguists are in agreement that humans employ conceptual metaphors to form the abstractions that are a standard feature of every language (verbal).
3 Obviously, Science has shown conclusively that Human Logic ≠ Material Logic. Mathematics provides a far better metaphor of understanding. Ironically however, moderns have attempted unsuccessfully to project Material Logic upon the Human World. Both ancients and moderns have mistakenly equated Life and Matter. An abundance of evidence, including my research, indicates that they are two, not one – an interactive duality, neither isolated, nor monistic.