Section Headings
If Material Interactions are Automatic & All is Matter, how about Choice?
Life requires Dynamic Meaning for Choice
Data Stream Derivatives: Ongoing Dynamic Meaning
Material Behavior: only First Two Derivatives significant
Living Behavior: All Data Stream Derivatives significant
Synopsis
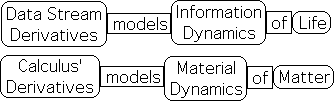
The internal logic of both Calculus and DSD is based upon derivatives, i.e. rates of change. Calculus is the prime mathematical tool of the Material Sciences. Its differential equations are employed to predict the behavior of Matter with great precision. However, the sizes of the changes in Calculus are infinitesimally small in that they have no dimension. Because there is no space between the successive points, there is no possibility of Choice. In contrast, DSD seems designed to accommodate the monitor-adjust process of living systems that is inherent to Choice. Further, the LA’s overlay process is ideally suited to generate dynamic meaning from raw data streams. If Calculus is the Mathematics of Matter, then Data stream Dynamics could be considered the Calculus of Dynamic Meaning.
Introduction to Derivatives
Derivatives are a key feature of Data Stream Dynamics. Data stream derivatives share some similarities with the traditional derivatives of calculus. The two types of derivatives also have some significant differences. To better understand these similarities and differences, let us first discuss the concept of a derivative.
A derivative is a rate of change over time.
On the most fundamental level, a derivative is a rate of change. It is called a derivative because it derives from some kind of change that occurs over time. This time can be real or mathematical, in the sense that it is an abstraction. On the most fundamental level, a rate of change/derivative is a ratio: the change in location over a change in time.
![]()
Infinite number of derivatives
Derivatives also change over time. As such, it is possible to compute a higher-level derivative to characterize this rate of change. Because this process can be extended indefinitely, there are an infinite number of derivatives. Derivatives epitomize the Buddhist notion that all is change. Derivatives are helpless before the static world.
Living Algorithm derivatives for Life; Calculus derivatives for Matter
The Living Algorithm’s sole function is to produce the rates of change/derivatives of a data stream. However, these derivatives are not like the traditional derivatives of calculus. A basic difference is that data stream derivatives are discretized, i.e. broken into discrete parts, while the derivatives of calculus are continuous. As such data stream derivatives do not require the mathe-magic of calculus, but instead only require common sense arithmetic. Second, data stream derivatives are not meant to model the changes/dynamics of material systems, but are instead meant to model the changes/dynamics of information digestion in living systems. In brief, the derivatives produced by calculus specialize in Matter, while the Living Algorithm’s derivatives specialize in Life.
Traditional derivatives computed via calculus’ mathe-magical processes, hence intimidating
Traditionally, 'derivative' is the mathematical term for an instantaneous rate of change. Calculus is a complicated mathematical process designed to compute derivatives, these instantaneous rates of change. By taking an infinite sum of these infinitely small derivatives, mathematicians regularly come up with something. This mathe-magical process is at the heart of calculus and could be why the word 'derivative' is intimidating to those with a non-mathematical mind.
Let’s look a little deeper into the differences between the derivatives of calculus and the Living Algorithm’s data stream derivatives. We begin with a discussion of calculus.
The Fundamentals of Calculus
Differentiation produces Derivatives: Instantaneous Rates of Change
Calculus is the mathematics of change. Calculus has two basic processes, differentiation and integration. The first, differentiation, breaks a continuous line into infinitesimal parts, derivatives. Because these derivatives are infinitely small, they represent instantaneous rates of change. Differential calculus, one branch of this immense topic, contains many complicated mathematical processes designed to compute derivatives, these instantaneous rates of change.
Integration: an infinite sum of infinitely small derivatives to come up something
Calculus’ second process is integration. As the name suggests, integration puts these infinitesimal parts back together again. Infinitesimal derivatives have a size of 0, by definition. When we add an infinite number of these infinitely small magnitudes together, we come up with a concrete magnitude. Integration is the mathematical term for this infinite summation. Integral calculus, another branch, contains many complicated mathematical processes designed to integrate these instantaneous derivatives. The integral sign, ∫, is employed to indicate the process of integration. Reiterating for retention: differentiation and integration are the two basic processes of calculus. As they deal with infinity, these processes are mathe-magical in nature.

Instantaneous derivatives ideal for describing Instantaneous Matter
Instantaneous derivatives are ideal for describing the material world, which also operates instantaneously.
![]()
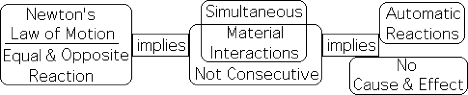
Newton's Law of Motion: Automatic Processes, no Cause & Effect, with Instantaneous Matter
Isaac Newton described this instantaneous feature of matter in his famous law of motion that stated: for every action, there is an equal and opposite reaction. The subtext of this law is straightforward: material interactions occur simultaneously, rather than consecutively. Newton’s law implies that all action in the material plane happens instantaneously, not one after the other, as is required for cause and effect. In other words, there is no such thing as cause and effect, just automatic processes. This notion would be hard to believe except for the abundance of evidence that supports it. The mathe-magical processes of calculus resolve this counterintuitive notion.
Differential equations, a combination of differentiation and integration, employed to characterize all material interactions.
Differential equations, another branch of calculus, combine derivatives and integration in one equation. Scientists employ differential equations to describe all material interactions.
“The laws of inanimate things are now well understood. They take the form of differential equations, which describe how interlinked variables change from moment to moment, depending upon their current values. … They represent the most powerful tool humanity has ever created for making sense of the material world. Sir Isaac Newton used differential equations to solve the ancient mystery of planetary motion. In so doing, he unified the earthly and celestial spheres, showing that the same laws of motion applied to both.
In the nearly 350 years since Newton, mankind has come to realize that the laws of physics are always expressed in the language of differential equations. This is true for the equations governing the flow of heat, air, and water; for the laws of electricity and magnetism; even for the unfamiliar and often counterintuitive atomic realm, where quantum mechanics reigns.” (Steven Strogatz, The Joy of X, pp. 155&158, 159)

Due to the importance of differential equations, years of calculus are a must to understand the dynamic interactions of the continuous, hence instantaneous, world of matter.
If Material Interactions are Automatic & All is Matter, how about Choice?
All Material Interactions are Automatic
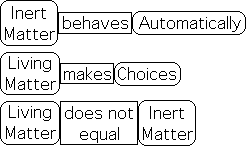
An abundance of evidence indicates that all material interactions fall under the sway of differential equations, which behave automatically, instantaneously, without cause and effect. The conclusion is inescapable: all material interactions are automatic. If the Universe consists of nothing but matter, then the entire Universe is on automatic - dominated by interactions revealed by differential equations.
![]()
If all is Matter, then there is no choice.
This materialist perspective eliminates the possibility of choice. However, this necessary conclusion is based upon the postulate that even living systems consist solely of matter.
![]()
If Living Matter exerts choice, then it is not only Matter
The next conclusion is equally necessary. If living systems are able to exercise choice between alternatives, then they must consist of something in addition to matter. Aaaeeiiii! The dungeon creatures rattle their chains, screaming for freedom, as the Establishment hires more guards.
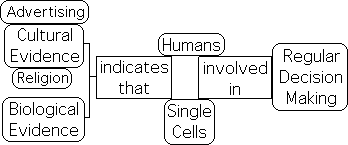
An abundance of evidence indicates that humans & cells are involved in decision-making.
An abundance of evidence indicates that living matter is involved in a nearly continual process of making choices. Religion, advertising, and elections are just a few of the institutions that have arisen to influence our human ability to choose between alternatives. It seems that even the single cell, the basic unit of Life, is involved in decision-making. Stanford biologist, Dr. Bruce H. Lipton states:
"Each cell is an intelligent being that can survive on its own. … They actively seek environments that support their survival while simultaneously avoiding toxic or hostile ones. Like humans, single cells analyze thousands of stimuli from the microenvironment they inhabit. Through the analysis of this data, cells select appropriate behavioral responses to ensure their survival.” (Biology of Belief, 2008, p. 7)
Life must have another component.
The evidence seems to be irrefutable. Living matter makes choices. Matter behaves automatically. Life consists of Matter, but does not equal Matter. Life must have another component besides the material one. But what?
Life requires Dynamic Meaning for Choice
Interested in animate systems, not the inanimate systems of calculus
It is evident that calculus’ differential equations, which combine the complicated processes of differentiation and integration, are able to precisely describe the behavior of the material universe. This is certainly an amazing feat. However, we are not interested in the inanimate world of matter. We are only interested in the animate world of life, the realm where choices seem to be made.
Is there a mathematics of change/calculus for human beings?
Is there a calculus of living systems? A mathematics of change that applies to human beings? Not our material component. The above discussion indicates that all matter is on automatic. We are interested in the aspect of humans that have the potential for choice.
Not our material component
If you are of the traditional scientific mindset, you might wonder: What else is there besides matter?
How about art, music, culture, sports, politics, religion, family, the quest for self-realization, and love?
What do material-based explanations have to reveal about these significant features of human existence? Not much. Although the matter specialists can tell us precisely how an individual atom will behave, this does not provide us with any meaningful information concerning the more subtle aspects of our lives.
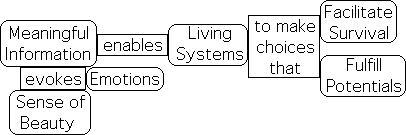
Humans & other living systems thrive on Meaningful Information.
And this is the point. We humans, as well as many other life forms, thrive on meaningful information. We crave information concerning our environment to fulfill potentials, including survival. Further all the significant human pursuits mentioned above are also based in the transfer of meaningful information from one individual or group to another. This is in direct contrast to exclusively material systems. Because it behaves automatically, inert matter has no use for information.

Traditional Information Theory addresses Information without Meaning
Is there a mathematics that deals with meaningful information?
Traditional information theory, of course. Shannon developed the mathematics behind this theory over a half century ago.
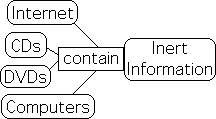
Wrong. Traditional information theory only addresses inert information, such as that contained in electronic transmissions.

This discipline does not include the meaningful information that interests us. Machines, such as computers, only employ and manipulate inert information. Living systems are required to impart some type of meaning to inert information. Put another way: without Life to impart meaning, information remains inert.

Electronic digital information is inert without humans to impart meaning.
For example, the information contained in electronic form in CDs, DVDs, and the Cloud is inert. It is useless, unless it is first translated into some type of sensory information, for instance sound. This sensory information is equally useless, unless there is a sensory organ to translate the information into an understandable form, an ear for instance. Further, even the sensory information remains garble unless we somehow impart meaning to this inert information. Witness the sleeping human or someone in a coma. The senses might be operating on minor level, but there is nothing to invest the information with significant meaning.
Meaningful information employed to make choices
Information is inert without meaning. Meaning animates information – turning it into a form that is relevant to living systems. On the most basic level, Life might employ meaning to make choices that facilitate survival or fulfill potentials. On more subtle levels, meaningful information might evoke an emotion, a sense of beauty or excitement.
Electronic Information contains Potential Meaning
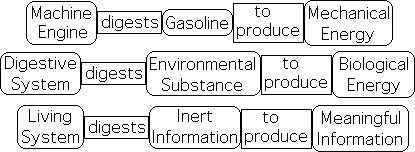
Electronic bits certainly have an abundance of potential meaning. However, this potential meaning is equivalent to oil’s energy stored in the earth’s bowels or the nuclear energy stored in an atom. There must be a mechanism to release the energy. For instance, oil must be extracted from the earth and then converted into a usable form, say gasoline. That is not all. A machine, for instance a car, is required to extract energy from gasoline.
Life must digest Inert Information to transform it from potential to actual meaning.
Our digestive system provides another example of transforming the potential into the useful. An abundance of potential biological energy is stored in plants and animals. A living system must digest the food to convert it into nourishment. In similar fashion, a living entity must digest inert information to transform it into meaningful information. For instance, a human must digest the isolated electronic information contained on a CD, DVD or a computer to turn it into the meaning of music, a motion picture, or words. In each of these cases, the original substance, whether gas, food, or information, is not translated into another language, but is instead transformed into a useable form. It seems that living systems have the ability to digest both organic substance and inert information. This digestion process transforms these 'substances' into a more useable form. Material systems do not have this capacity.
Living Systems impart Meaning by understanding Changes.
The scientific community has a fairly complete understanding of the conversion process associated with gasoline and mechanical energy. They also understand the many aspects of biological digestion. But what about information digestion? How do living systems digest information? A living system, such as a human being, must digest the information in some way to provide it with meaning. What features does meaningful information have? What is the difference between inert information and meaning infused information?
Living systems impart meaning to static information by understanding the changes it goes through in relationship to itself and other information. For instance, we must have some way of knowing whether the inflection of a sentence is moving up or down to know if a question is being asked or not.

Meaningful Information is Dynamic, not Static like Electronic Information.
'Dynamic information' is what we call this understanding of the changes of inert information.

Understanding the dynamic changes and relationships of information reveals meaning to the organism. As such, it is a reasonable postulate that meaning is derived from dynamic information. Again, not dynamic in the sense of a circling DVD turned into electronic dots on a TV set. Each of these bytes of information is isolated with regards to each other. This is why we can copy, pause, rewind, playback, and replay our digital information.
![]()
History is the prime Difference between Static and Dynamic InformationMeaning = Information with History
In contrast to the static nature of digital information, the dynamic information associated with meaning is connected to what went before. In other words, dynamic information/meaning has a history. The current meaning has some kind of relationship to what went before. There is some type of connectivity between the present input and past knowledge. A machine, say a CD player, cannot supply this relationship.
![]()
Life digests Inert Information, transforming it into Dynamic Information
How does this transformation process occur? How do we invest static information with history? How are we able to understand the changes it goes through?
Living systems must have some type of mechanism to digest information. A stomach digests organic substances commonly called food. This process does not translate it into a new language. The digestion process transforms it into a new form, such as fat, proteins or carbohydrates. The Body then employs this digested food to run its biological systems. In similar fashion, we suggest that Life must have a method of digesting information. This information digestion process does not just translate binary bits into another language, but instead transforms it into a form that Life can invest with meaning.
![]()
The Living Algorithm creates Dynamic Information (Inert Information with History)
An abundance of evidence suggests that the Living Algorithm provides the algorithm by which static information is transformed into a meaningful form. The Living Algorithm’s digestion process provides a stream of information with history. The same process provides current knowledge about the changes/dynamics the information is going through.
![]()
Mathematics of the Moment Notebook: Living Algorithm uniquely suited to be Life's Computational System
We devoted an entire monogram/notebook, Mathematics of the Moment, to establish that the Living Algorithm's algorithm is uniquely suited to addressing the unique computational needs of living systems. In brief, Life requires a relatively simple computational system with low memory needs that can provide up-to-date information about the ongoing flow of environmental data streams. This information must contain measures that both describe the present moment in relationship to past moments and simultaneously make some kind of prediction about what the future may hold. The techniques of Probability, Physics, and Digital Information Processing were inadequate to this task. Only the Living Algorithm's algorithm met all of these requirements, and more.
Data Stream Derivatives: Ongoing Dynamic Meaning
We can now pose a plausible answer to our original questions: 'Is there a calculus of living systems? A mathematics of change that applies to human beings?' Data Stream Dynamics, the mathematical system produced by the Living Algorithm, could very well be the calculus of living systems - the mathematics of change that applies to human beings. Let's see what the implications are.
Discretized Information vs. Continuous Matter
In contrast to the continuous world of matter that calculus' differential equations describe so well, the mathematical world of information digestion as defined by the Living Algorithm's algorithm is discretized. In other words, the information that the Living Algorithm digests comes in discrete chunks and is not continuous at all. Ironically, the subatomic world of electrons and photons is also discretized into the elementary quanta of individual photons and electrons. For instance, electrons do not move continuously, but instead jump from shell to shell, never inhabiting the in-between space.
Discretized Data Stream Derivatives vs. Instantaneous Material Derivatives
In the current study of information digestion, we expand the notion of derivatives to include non-instantaneous rates of change that are required of a discretized world. Instead of the mathe-magical process of calculus, the rates of change in the world of information digestion are all computed with a simple subtraction.
Velocity & Acceleration: the 1st 2 derivatives
This process accords with our common sense notions of the first 2 derivatives, velocity and acceleration. Velocity is the 1st rate of change, the 1st derivative. Velocity is the measure of the change of location over time - how quickly we travel from one location to another. We compute this velocity/speed with a simple subtraction – final destination minus the starting point, also noting how long it took. Acceleration is the rate of change of this rate of change, the 2nd derivative. In other words, acceleration is a measure of how quickly velocity changes. We could also compute the acceleration with a simple subtraction - the ending velocity minus the initial velocity, also noting how long it took. For instance, when a car's velocity changes from standing (0 MPH) to 100 MPH in 10 seconds, it is said the car accelerates 100 MPH in 10 seconds.
Derivatives based in larger time increments are averages of smaller time increments.
In each of the above examples, the amount of time was finite. As such it is an approximation of moment-to-moment acceleration. For instance, if we examine the velocity changes in smaller and smaller increments, the acceleration might vary significantly, for instance slower at the start and more quickly at the end. Hence the difference in location over the larger time increment is just an average of all the smaller increments, which could vary individually. The smaller the time increment, the more precise the derivative.
As the time increment & distance traveled approach 0, the rate of change remains constant.
To provide accurate formulas for material dynamics, science required an exact velocity from moment-to-moment. To achieve this miraculous feat, they took smaller and smaller time increments. As the time increments approaches 0, the change in distance also approaches 0. However, the two values, time and distance, approach 0 at a similar rate. Hence their ratio, the rate of change, remains consistent, even though the increments become smaller and smaller. (To distinguish the exact instantaneous 1st derivative from the less exact average, scientist/mathematicians call the first measure 'velocity' and the second measure 'speed'.)
Derivatives of calculus based upon differences between adjacent points.
Calculus is the mathematical method by which the finite ratio of these infinitesimally small distances and time durations is computed. Hence, at all times, even on the infinitesimal level of calculus, derivatives such as velocity and acceleration are computed via a subtraction of location to location over an infinitesimally small time increment.
Instantaneous Material Derivatives isolated from the Past.
Each of these locations is independent, with no relationship to what went before. As such, the instantaneous derivatives only characterize the individual moment, but have nothing to do with what went before. Equations are derived that model the automatic processes of matter, but material derivatives have no connection to the past. They are independent readings. This information from the material derivatives is inert – without history and meaning. Humans must digest this inert information to give it meaning. Note in the diagram below that each of the derivatives is based upon a simple difference between adjacent locations.
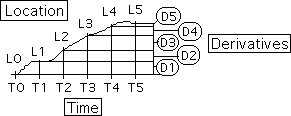
Data Stream Derivatives intimately connected to the Past
In contrast with this isolation, the derivatives in data stream dynamics are intimately connected to the past. Just as with material derivatives, data stream derivatives are also computed via a subtraction of quantities over time. However, instead subtracting location from location, data stream derivatives are based upon the difference between the most recent data point (the location) and the prior derivative. This creates a new derivative, which is a mixture of data and derivative. This synthesis generates a deep relationship between the present and the past. The current data stream derivative is a blending of all the data that went before, not just the surrounding data points (locations). Below is a picture of the interconnections between the data points and the data stream derivatives.
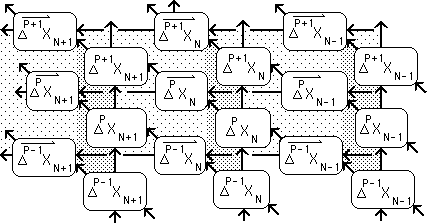
Calculus Derivatives isolated; Data Stream Derivatives connected
In other words, the mathematical processes of calculus create derivatives that are isolated from each other and the past. This isolation is especially appropriate to material interactions, which seem to be based solely upon the automatic processes of differential equations. In contrast, the mathematical processes that produce data stream derivatives are especially designed to connect the past with the present in an ongoing fashion. Besides remaining in the finite realm, data stream dynamics relates the current moment with past moments.
Differences between Calculus Derivatives and Data Stream Derivatives
Let us summarize the significant divergences between the derivatives of matter and information digestion. The derivatives of calculus are based upon the difference between consecutive data points, while data stream derivatives are based upon the difference between the data point and the most recent derivative.
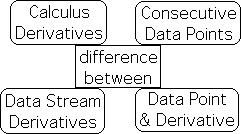
The derivatives of calculus are continuous and instantaneous, while data stream derivatives are incremental and finite. Let us see what the implications are.
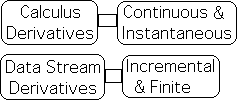
Incremental nature of data stream dynamics enables possibility of choice for Living Systems
These differences render data stream dynamics more appropriate to living systems. As noted, the continuous and automatic processes of material dynamics eliminate cause and effect, monitor and adjust. However, living systems require a give and take, monitor/adjust relationship with their environment in order to fulfill potentials, including survival. The incremental, vs. continuous, nature of data stream dynamics provides that opportunity. The finite nature of the time increments allows for the necessary 'wiggle room' to monitor and adjust to external stimuli.
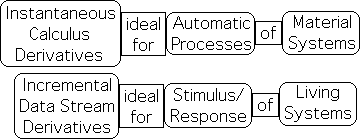
Living Algorithm System produces Dynamic Information from Inert Information
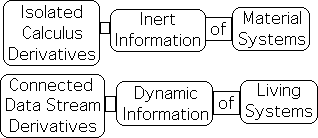
Further, the interconnectivity of the past and present produced by data stream dynamics provides a context that living systems also require to provide history and thereby meaning to information. The information concerns the changes between the data in relationship to the past. As such, the Living Algorithm that is at the heart of data stream dynamics produces dynamic information, not the inert information of calculus.

Calculus produces isolated derivatives, hence inert information, that is appropriate for material systems. The dynamic information of data stream derivatives is ideal for living systems.
Material Behavior: only First Two Derivatives significant
Infinite number of Derivatives
As noted, we compute velocity and acceleration with a simple subtraction. In similar fashion, we could also compute the acceleration's rate of change, how quickly acceleration changes – the 3rd derivative. This process can be extended forever. As such, there are an infinite number of derivatives. We can apply the same essential process to both material and information dynamics. Calculus' mathe-magical process is required to determine material derivatives, while basic arithmetic processes determine data stream derivatives. However, both are rates of change over time. As such, we can compute derivatives of derivatives of derivatives ad infinitum with either process - simple or complex.
Despite this proliferation of derivatives, only the first two, velocity and acceleration, are of primary significance in the continuous world of matter. The higher derivatives, i.e. thrust, etc, barely have names, indicating their lack of importance.
Force is a Function of Acceleration in Material Dynamics.
The emphasis on acceleration in the material world is due to the fact that forces are a function of acceleration. Isaac Newton’s famous equation states that force equals the product of mass and acceleration, F = m*a. This equation is of prime importance in the physics (dynamics) of matter.
All other equations in Physics derive from Force Equation.
As in indication, those individuals that are in the industry of material sciences sometimes jokingly say that this is the only equation you need to know. In other words, all the other complicated equations of Physics derive from this simple expression. The subtext is simple: the product of mass and acceleration is at the heart of all the intricate material interactions.
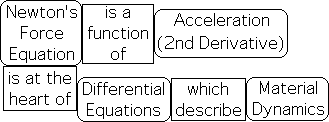
There is no need to understand the higher derivatives because the product of acceleration and mass reveals all that you need to know about the dynamics of matter.
![]()
Living Behavior: All Data Stream Derivatives significant
Conversely, the higher data stream derivatives are of great significance in the discretized world of information digestion. They even have their own name, Liminals.
Author initially dismisses higher data stream derivatives.
Possibly due to the Author’s training in Physics, he too dismissed the higher derivatives as inconsequential for nearly 2 decades after he first uncovered the existence of data stream derivatives in his Data Stream Momentum phase of 1994. His earliest studies initially confirmed this notion.
Data Stream Dynamics contains scalar derivatives and directed derivatives.
First, a little background. The dynamics of matter has one type of derivative. In contrast, the dynamics of information has two types of derivatives, deemed the Deviation and the Directional. The Deviation, which reveals the probable range of deviation of a data stream, is a scalar (a quantity). The Directional, which reveals the directional tendencies of a data stream, is directed, a 'vector'. Both derivatives derive from the Decaying Average, the data stream’s velocity, first uncovered in 1978. To facilitate understanding, we likened the data stream derivatives to a family with the Living Average as the mother of both the Deviation, her son, and the Directional, her daughter. Each of the children has their own family of higher derivatives. In other words, data stream dynamics contains both scalar derivatives and directed/'vector' derivatives.

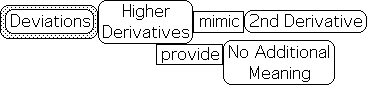
Higher scalar derivatives provide little meaning.
In his investigations of the son’s scalar side of the family, the evidence indicated that the Deviation’s higher derivatives seemed to simply mimic the 1st Deviation. As such, they revealed no new information and hence were considered inconsequential. Preliminary investigations into the Directional’s side of the family were ambiguous. Strange things were going on, but the Author had no idea what to make of it.
Then in his Creative Pulse phase of 2002, the Author first uncovered the mysterious significance of the Directional, the data stream’s vector acceleration. It seemed to be somehow linked to Attention and a productive/creative session. Although he graphed the higher derivatives, he still had no clue as to what was going on.
Higher 'vector' derivatives, the Liminals, seem to mimic subconscious mental processes.
Finally, a few years into his Information Dynamics obsession of 2010, he noticed that the Liminals, the Directional’s higher derivatives, did not mimic the 1st Directional, but instead seemed to provide additional meaning.

The Triple Pulse, a visualization of the first directed derivative, seems to model the alternation of Consciousness and Sleeping. In contrast, the behavior of the Liminals, the higher derivatives, has similarities with the unconscious cognition of dreaming. In other words, the 1st derivative is related to Conscious mental activity, while the higher derivatives/Liminals are somehow related to the subconscious mental activity, unconscious cognition. The concepts, while related to mental activity, are entirely different.
Core Concept Approach to teaching based upon the 10-minute rule.
Then came our momentous investigation into the Core Concept vs. Continuous approach to instruction. Experimental research has shown that humans have the ability to pay attention for about 10 minutes. This is called the 10-minute rule. Acknowledging the power of this unavoidable cognitive phenomenon, Dr. Medina created a teaching technique to take advantage of its properties. The Core Concept Approach, as we call Dr. Medina's technique, consists of breaking a lecture into a series of 10-minute segments, with each segment focused upon a single core concept.
Continuous Approach & the 'Eyes Open; Nobody Home' Phenomenon
The Core Concept Approach was developed in response to an alternate, yet traditional, teaching technique, the Continuous Approach. In this technique, new information is presented in a continuous fashion without definition. Experiments have shown this technique to be unsuccessful. Although the audience/students might appear to be awake, they don't retain the presented information. We call this the 'Eyes Open; Nobody Home' Phenomenon.
2 Data Streams chosen to simulate 2 Teaching Techniques. Data Stream Derivatives examined.
To compare these contrasting teaching techniques, we chose 2 data streams, whose length and total magnitude are equivalent. One data stream was chosen to simulate Dr. Medina's Core Concept Approach; the other data stream was chosen to simulate the Continuous Approach. We then compared the directed/'vector' derivatives of each data stream to see what they revealed. The results were startling to say the least.
Continuous Derivatives suggest 'Eyes Open; Nobody Home' Phenomenon
The derivatives of the Continuous Approach data stream both simulated the experimentally confirmed 'Eyes Open; Nobody Home' Phenomenon and provided a plausible cognitive mechanism for its occurance. The data stream's acceleration, the 2nd derivative, was steady and consistent. Prior papers on sleep found patterns of correspondence between a positive data stream acceleration and consciousness. If these associations hold, it indicates that the audience is at least awake, as is the case with the Continuous Approach to teaching.
Gravity, a constant acceleration, an influential force
Just as Consciousness is associated with the 2nd data stream derivative, gravity is also associated with calculus' 2nd derivative, acceleration. The force of gravity is the product of a constant acceleration and mass. This constant acceleration dominates our physical landscape: keeping us bound to the Earth and propelling the Sun, Moon, and Stars in their respective trajectories through the sky. Gravity is a truly powerful force.
![]()
Consciousness, a constant acceleration, but devoid of comprehension
It might seem as if the data stream's acceleration is equally powerful, as it is associated with consciousness. Not so. Although the audience is conscious during the Continuous Approach, experimental evidence indicates that there is no comprehension or integration of the presented material. Why? The mathematical model makes an interesting suggestion in this regard.
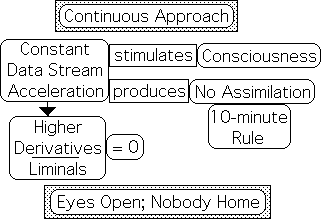
The Mathematics of the 'Eyes Open; Nobody Home' Phenomenon
When the data stream acceleration is constant, all the higher derivatives, the Liminals, equal 0. This is also true of the force of gravity. This is one reason that the scientific community pays so little attention to the higher derivatives of calculus. As mentioned, the Liminals are associated with unconscious cognition, subconscious mental activity. Unconscious cognition is associated with integration and assimilation of environmental stimuli. If unconscious cognition is shut down, all the Liminals equal 0, due to a continuous flow of information without definition; new information is no longer assimilated. Most of us have experienced this 'Eyes Open; Nobody Home' Phenomenon at one time or another. Experimental results regarding the 10-minute rule confirm these results.
The Mathematics of the Core Concept Approach
The derivatives of the Core Concept Approach simulate the advantages of this teaching technique. Instead of being constant, the acceleration of the Core Concept Approach proceeds in pulses. Prior papers have associated these pulses with pulses of attention, akin to the 10-minute attention span suggested by the 10-minute rule. Because the data stream's acceleration is constantly changing, the Liminals, the higher derivatives, are also continually changing. These highly active Liminals suggest that subconscious mental activity is equally active. Maximizing the potentials of unconscious cognition maximizes the assimilation and integration of information. Dr. Medina's many accolades as a teacher serve as evidence for the success of this approach.
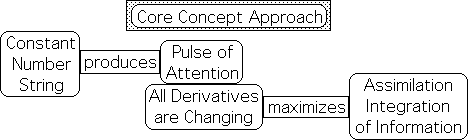
Constant Content maximizes Derivative Change; Changing Content minimizes Change.
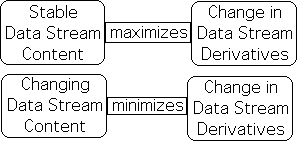
To simulate the Core Concept Approach, we chose a data stream consisting of three different Number Strings. A Number String consists of identical numbers. Ironically when a data stream's content remains consistent, it maximizes the changes in the data stream derivatives, but just for a pulse, not indefinitely. In other words, consistent content maximizes change. In contrast, a constantly changing content, as we had in the Continuous data stream, minimizes change in the derivatives. This counter-intuitive result is highly significant. Because our unconscious cognition thrives on changes in the data stream derivatives, and shuts down when there are no changes, assimilation and integration are maximized when the lecturer's content is held to a single core concept.
Higher Derivatives significant to Living Matter; Insignificant to Inert Matter.
It is evident that the higher data stream derivatives, the Liminals, are quite significant to living systems. Active Liminals seem to be somehow associated with our cognitive ability to assimilate and integrate new material. In contrast, the higher derivatives in calculus are overshadowed by acceleration, the 2nd derivative, as a way of describing the behavior of matter. This is just one difference between data stream derivatives and the derivatives of calculus.
Summary of Differences between Derivatives of Calculus & Data Streams
In summary: derivative are rates of change: change of location over the change in time. The derivatives of calculus, which apply so well to the behavior of inert matter, are continuous and isolated from the past. Data stream derivatives, which apply so well to the behavior of living matter, are discretized and intimately connected to the past.