Synopsis
Scientists typically apply the word quantized to the Subatomic Realm. The word indicates that the values of certain variables, e.g. those associated with electron rings, are limited to a specific set of numbers rather than being continuous. The intent of this article is to show that the orbits of both planets and moons around a large central mass are likewise quantized. In this case, the distance, period and velocity of these satellites are all quantized. The evidence for this proposition comes in the form of 12 graphs. They indicate a distinctly linear relation between order and the log of the specified dimension. All the correlations between order and dimension are exceptionally high (over 98.5%). To characterize this prevalent and consistent astronomical phenomenon, we wrote an empirical equation deemed the Quantized Orbit Law. Thus far this quantization of orbits is a mystery. This tight order to our solar system, and by implication the Universe, indicates that the harmony of the spheres hypothesized by Pythagoras was correct.
Section Headings
- Harmony of the Heliocentric Spheres
- Quantized: Subatomic to Astronomic
- Evidence: the Quantized Orbits Graph
- Lunar Orbits: Quantized Distance
- Anomalies: Empty & Collective Orbital Rings
- Logarithmic Space
- Orbits: Quantized Period
- Orbits: Quantized Velocity
- Equation for Quantized Orbits Law
- Questions, Mysteries & Speculations
- The Titius-Bodes Law, Dermott’s Law & Planetary Resonance
- Summary
Harmony of the Heliocentric Spheres
Approximately five centuries before the Common Era, Pythagoras postulated that there was a simple harmonic relationship between the distances of the celestial bodies from the Earth – a.k.a. the ‘harmony of the spheres’. It is now commonly understood that the planets revolve instead around the Sun. While wrong in this regard, it seems Pythagoras was right concerning a simple harmonic relationship between the distances of the nine planets from the Sun. Rather than a harmony of the geocentric spheres, there is a distinct and pronounced harmony of the heliocentric spheres, i.e. the Planets.
Let’s examine this hypothesis in more detail.
Pythagoras began his scientific endeavor with music. He discovered that there was a simple mathematical relationship between the length of vibrating strings and the harmonies they produced. From this simple discovery, he made an inference that changed the course of Western civilization.
By his time, the Greeks knew that the firmament was populated by the Sun, Moon, Stars and the 5 visible Planets. Pythagoras postulated that each of these 8 entities occupied a distinct sphere that surrounded a fixed Earth. He further surmised that these 8 spheres had a harmonic relationship to each other, in similar fashion to vibrating strings. This famous theory is known appropriately as the 'harmony of the spheres' – geocentric spheres.
Two millennia later, Copernicus et al established that we instead live in a solar system where the planets revolve around the Sun rather than the Earth. Only the Moon revolves around the Earth and the Stars occupy remote galaxies hundreds, if not thousands, of light years away. This knowledge dispelled the overall Pythagorean theory, i.e. that we live in a geocentric system.
While not applicable to the Moon and Stars, it seems that the 'harmony of the spheres' does apply to the distance of each planet from the Sun. Considered from a logarithmic perspective, the distance between each of the planetary orbits is virtually equal. Because the variable can only assume only certain discrete magnitudes, it could be said that the distance between the Sun and its planets is quantized (more later).
Planetary Orbits Quantized
As well as the planets, this quantized step-like relationship also applies to the distances between the large outer planets, i.e. Jupiter, Saturn and Uranus, and their moons. As well as distances, this discretized harmony also applies to both the orbital periods and velocities of both the planets and moons about their immense central mass, whether the Sun or outer planets. When smaller masses, whether planets or moons, revolve about a large central mass in our solar system, the distance, period and velocity of their orbits are all seem to be quantized. Put another way, three components of an orbit are quantized. Due to the widespread applicability of this principle throughout our solar system, i.e. quantization of distance, period and velocity, this striking harmonic relationship might even surpass Pythagorean expectations.
Universal Law: Planetary Orbits are Quantized
While the orbits of moons and planets in our solar system seem to be quantized, this orderly relationship does not seem to apply uniformly to the rest of the Universe. Indeed Dr. Lars Bildsten, head of the esteemed Kavli Institute for Theoretical Physics at the University California in Santa Barbara, said in an interview that this orderly quantization is quite unusual. He continued by saying that the planets in most solar systems either are gradually spiraling into or away from their respective suns.
A visiting researcher at the Physics Institute who is searching for solar systems that might sustain life had something to add to the mystery. She said that the stability and orderliness of the orbits in our particular solar system was a definite factor in the origination of Life. The 4 billion years long astronomical regularity enabled evolution. When orbits change, even if ever so slightly, over millennia, as they do in most of the rest of the Universe, the deviations of heat and climate are too great for evolving living systems to adapt of environmental conditions. Life requires stability to evolve.
Let us develop these ideas in more detail – starting with some definitions, following with the evidence, and concluding with some speculations.
Quantized: Subatomic to Astronomic
Quantized Planetary Orbits?
Quantized Planetary Orbits? What could this peculiar arrangement of words possibly mean?
Quantized applied to Subatomic Realm
The word ‘quantized’ is typically applied to the mysterious Subatomic Realm. For instance, an electron’s orbits are quantized; or light is quantized into discrete energy packets called photons. Quantum mechanics applies to the Subatomic Realm.
Contrasted with continuous Atomic Realm
The word arose to express a contrast with the Molecular Realm, where phenomena tend to be continuous, i.e. not quantized. For instance, matter’s motion is continuous and gravity’s force is continuous. Traditional calculus was developed to deal with the appropriately called space-time continuum.
Quantum Theory developed to deal with quantized Electron Rings
In the early 20th century, scientists were surprised to find that electrons could only occupy certain discrete orbits about an atom’s nucleus, but not the space in-between. This discovery violated the notion of continuous space. They eventually discovered that the behavior of the entities inside an atom behaved in a quantized, rather than continuous fashion. Quantum theory along with its own mathematical system was developed to deal with the Subatomic Realm.
Quantum Physics Definition of Quantized
In this context, the word is defined as follows:
“Quantized (verb; Physics): applying quantum theory to, especially form into quantity, in particular restricting the number of possible values of (a quantity) or states of (a system) so that certain variables can assume only certain discrete magnitudes.”
General definition of quantized: Restricted Values, not continuous
This definition of the word is distinctly restricted to the micro world of quantum theory and the Subatomic Realm. We are going to employ the definition in a more general sense to apply to the macro universe of planetary orbits. Leaving off the micro references, we define the word in the following fashion:
Quantized (verb; General): “restricting the number of possible values of a quantity or states of a system so that certain variables can assume only certain discrete magnitudes.”
Definition applies to Universal Law of Quantized Orbits
Under this definition, multiple orbits in a gravitational system are quantized as “certain variables, i.e. distance, period, and velocity, can assume only certain discrete magnitudes.” As we shall see, the number of possible values of these variables is severely restricted. Conversely, the possible values of the variables associated with planetary orbits are not continuous. This finding is so definitive that we boldly deem it, not just a hypothesis, but rather the Law of Quantized Orbits, even though it only applies to our solar system.
As we inhabit a continuous space, Quantized Space counterintuitive
Just as the micro universe of electron rings and photons is quantized, so is the macro universe of gravitational orbital systems also quantized. Although the scientific community has grown accustomed to this feature in the Subatomic Realm, quantized, i.e. non-continuous, space is shockingly counterintuitive on both the micro and macro levels. Although science fiction writers invent time warps and vortexes in space that enable their characters to circumvent continuity, space and time are always continuous in the Atomic Realm that we inhabit. Despite our hopes and imagination, physical bodies are never able to jump discontinuously from place to place. Despite the logical possibility, electrons can only inhabit certain quantized rings about the nucleus of an atom; and moons and planets can only inhabit certain quantized rings moving at a quantized velocity over a quantized period of time about a large central mass.
Easier to accept Quantization in Subatomic Realm because separate from Atomic Realm
Strangely enough, it is much easier for scientists to accept that the notion that an atom’s interior is quantized than it is to admit the proposition that planetary orbits are quantized. Why? The Subatomic Realm occupies a unique micro space that is inside the Atomic Realm where we reside. Further the residents and characteristics of the two realms are mutually exclusive. As such, it seems a reasonable proposition that the Subatomic Realm is quantized, while the Molecular Realm is not.
swirling gravitational systems part of continuous Atomic Realm: Newton + gravity
In contrast to the Subatomic Realm, the firmament with all of its swirling gravitational systems is a distinct part of the continuous Molecular Realm. Even though many strange creatures, i.e. black holes, dark matter and neutron stars, inhabit our Universe, virtually all celestial phenomena can be explained via Newtonian mechanics applied to the force of gravity. Because so many former mysteries have been explained in this manner, astronomers in general believe that traditional mechanics will eventually account for all mysteries including quantized orbits. For this reason, the group is exceedingly reluctant to entertain new possibilities.
Unsolved Problem: Continuous Atomic World & Quantized Orbits
Yet there are many unresolved difficulties with this position. Rather than quantized, both the Molecular Realm and force of gravity are continuous. Although gravity represents a curvature of space according the Einstein, this molecular space is still continuous. If the moons and planets exist in a continuous world, how is it possible that their orbits are quantized? This astronomical mystery remains to be solved.
As no current solution: deemed Quantized orbits
In the future, some ingenious individual may provide a Newtonian solution or not. This problem might require a different type of solution. Just as we don’t know why the Subatomic Realm is quantized, we may never know why the orbits in swirling gravitational systems are likewise quantized. Since there is no apparent solution to the dilemma at the current time, we will take the liberty of calling this astronomical phenomenon: the Law of Quantized Orbits.
Evidence: the Quantized Orbits Graph
What evidence supports this supposed Law of Quantized Orbits? Twelve Excel graphs that compare planetary order with empirical data regarding planetary orbits taken from Handbook of Physics and Chemistry, 1976.
Because of its importance, let us examine the components of these so-called Quantized Orbits Graph.
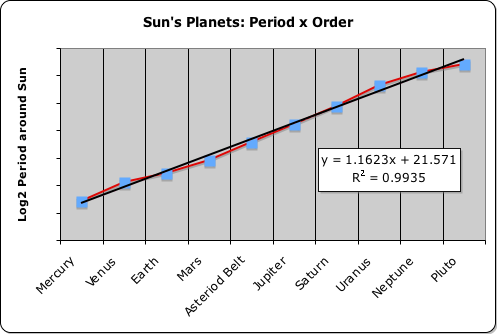
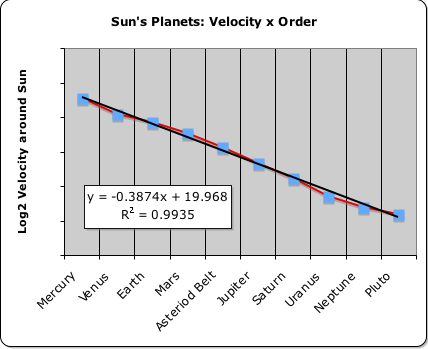
For our example, we will employ the following groundbreaking graph. It plots the interaction between planetary order and orbital distance from the Sun. This visualization particularly exhibits the Pythagorean 'harmony of the heliocentric spheres' that characterizes our solar system.
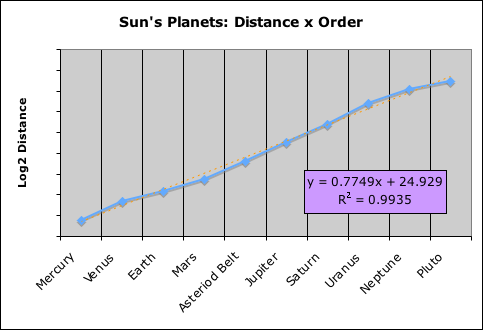
What are the graph's parameters? The horizontal axis indicates each of the nine planets and the asteroid belt. Each planet was assigned a number that represented its relative position from the Sun. For instance, Mercury is assigned a 1 because it is closest to the Sun. To make better sense of the data, we assigned a ‘5’ to the asteroid belt between Mars and Jupiter (more later). Under this schema, Pluto is assigned the number 10 rather than 9.
The vertical axis indicates a function of the distance of each planet from the Sun. Rather than miles, the figures on the left represent the logarithm base 2 of the planet’s average distance in kilometers from the Sun. (All orbital dimensions, whether planetary of lunar, come from Handbook of Physics and Chemistry, 1976, F-165.)
For instance, Venus is approximately 110 million kilometers from the Sun. The log base 2 of this number is ‘26.7’.
y-axis values = Log base 2 (planetary distance from Sun)
Planet’s Ordered Pair ≈ (Position, f (Distance from Sun))
Each planet is represented by an ordered pair on the graph – a Planetary Dot. The first number is the Planet’s numbered order from the Sun. The second number is a simple function of the Planet’s distance for the Sun (indicated immediately above). As the second planet, Venus is represented by the ordered pair (2, 26.7).
Two Lines: Black Line connects Ordered Pairs
The graph shows two lines – one blue, the other yellow. A blue line connects the Planetary Dots. A visual observation reveals quite clearly that there is a distinct linear relationship between these planetary distances and their relative order from the Sun.
Yellow Line: Perfect Fit Line
To visualize this observed relationship, we tabulated a statistical ‘best fit’ line between the planetary distances and their relative position from the Sun. This is represented by the yellow line. Again a simple inspection indicates a high correlation. For instance, it is even hard to tell that there are two lines at certain sections.
99% Correlation
How strong is this relationship? What is the correlation between planetary position and distance from the Sun? The purple box on the graph contains this information. On top is the equation for the best-fit line; on the bottom is R2, i.e. the linear correlation between solar distance and order. The correlation between the 2 parameters is 99.39% – high by any standards.
Conclusion: Equal distance function between planetary orbits
The Sun contains 99.99% of our solar system’s mass. In other words, the Sun’s individual mass is greater than the entire amount of planetary mass by five orders of magnitude. The remainder of our solar system’s mass seems to have organized itself in concentric rings around the Sun. We can draw an indisputable conclusion from these facts. When viewed from a logarithmic perspective, the distance between each of these orbital rings is virtually the same. As they are equally spaced with no significant mass in-between, this visualization clearly indicates that orbital distances of the planets from the Sun are quantized.
Whoa! Pythagoras Right
Simply amazing! With some slight modifications, Pythagoras was right. There is a ‘harmony of the spheres', albeit heliocentric. But watch out! There’s much more! Rather than applying only to solar distance, this orbital harmony is far more universal. To see why, let’s examine some more Quantized Orbits Graphs.
Lunar Orbits: Quantized Distance
Question: Other solar systems?
Our straightforward conclusion evokes several questions. Does this phenomenon apply to other solar systems? If there is a large central mass, will the smaller masses order themselves in regular bands about the larger mass? Will the distance between each of these bands be equal? According to the esteemed Dr. Bildsten, No. Each solar system is unique and must be evaluated individually.
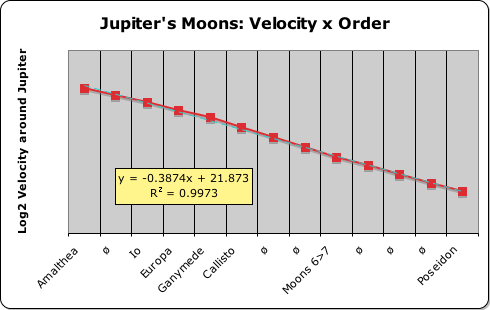
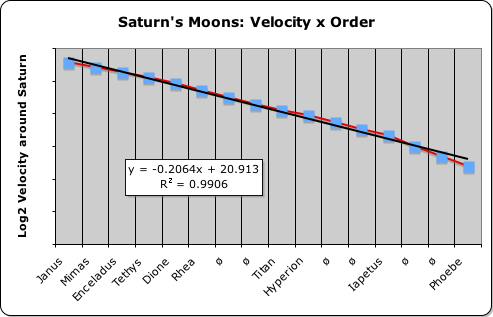
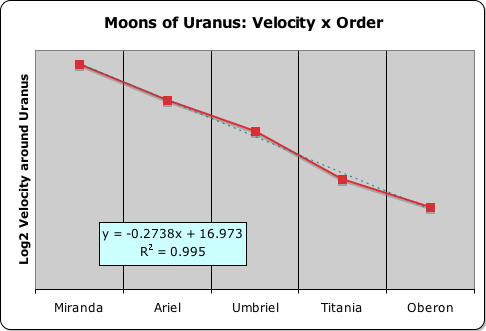
Although not necessarily applicable to other solar systems, this logarithmic rule certainly applies to the moons of Jupiter, Saturn and Uranus, as the following graphs illustrate. Notice that the best-fit line in each of the cases is nearly identical to the line connecting the Lunar Dots. Indeed the lowest of the 3 correlations between order and distance is 99.5%. Not too shabby! This level of correlation definitely meets the stringent standards of the Material Realm.
The discrete and equally spaced orbital distances indicate that planetary or lunar spheres do not coalesce in the space between the highly ordered rings. This restriction on location suggests that 'Orbital distances are Quantized', at least in our solar system.
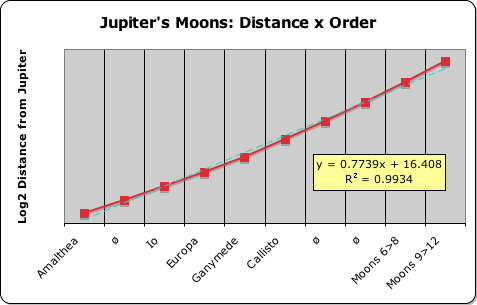
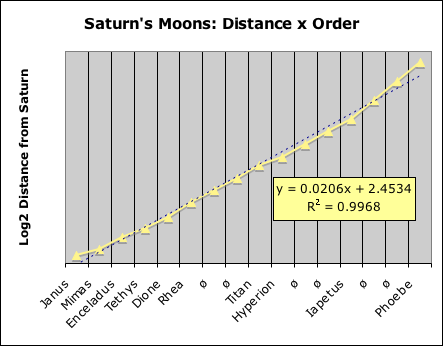
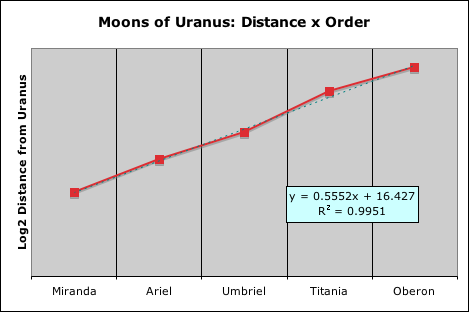
Anomalies: Empty & Collective Orbital Rings
Before proceeding forth to examine the orbit’s period and velocity, let us expose some anomalies. The horizontal axis of the graphs that visualize the distances of the moons from both Jupiter and Saturn require some explanation. Both contain the symbol ‘ø’ in some of slots rather than the name of moon, e.g. Titan. This symbol indicates an orbit that does not contain any evidence of a moon. What is our justification for this insertion? Our solar system contains a similar insertion.
Asteroid Belt? As 5th Planet eliminates Mars/Jupiter discontinuity
When we initially tabulated and considered the log planetary distances, there was a huge discontinuity between Mars and Jupiter. To eliminate this discontinuity, we chose to consider the asteroid belt as the fifth planet. Amazingly enough, the asteroid belt fit the planetary pattern perfectly. With this inclusion, a straight, rather than broken, line connected the log of planetary distances.
5th planetary Ring = gravitational fracture zone?
Due to this relatively perfect fit, the asteroid belt could be considered either an unformed or a shattered planet. Why didn’t this mass coalesce like the rest of the planets? Could this be because the 5th planetary ring (the asteroid belt) is a gravitational fracture zone between the smaller inner planets and the larger outer planets?
The second anomaly occurs in Jupiter’s graph. One slot contains the words ‘Moons 6>8’ and another ‘Moons 9>12’. Jupiter’s gravitational system contains 12 known moons. Moons 6 through 8 are a nearly identical distance from Jupiter. It is as if this collection of moons occupies the same orbit. The same holds true for Moons 9 through 12. Amazingly enough, these collective distances fit the quantized pattern, as the graph and correlation indicate.
Logarithmic Space
Each of these four graphs exhibits a readily apparent step-like pattern. The lines appear as gently inclined ramps, not erratic in any way. We achieved this regular linearity of planetary and lunar distances by considering space as logarithmic. What does ‘logarithmic space’ mean?
A common example will illuminate this bizarre notion. The Richter scale was developed to characterize the strength of earthquakes. Although the numbers range from 1 to 10, each increase, e.g. from 3 to 4, represents a 10-fold increase in magnitude. For instance, a level 6 earthquake is ten times as powerful and potentially devastating as a level 5 earthquake. In the parlance, an 8 on the Richter scale is an order of magnitude greater than a 7.
To achieve this clarity of expression, Richter applied the logarithmic function to real data. As such, the Richter scale could be considered logarithmic. Logarithms condense numbers in an exponential fashion. Due to familiarity, Richter’s numbers are the manner in which we understand the power of an earthquake. We don’t think of this power in terms of for instance pounds per square inch. Instead, newspapers report that Japan had a 6.2 earthquake on the Richter scale.
In similar fashion, our planetary and lunar distances have been logarithmically condensed. Due to this condensation, familiar terms like kilometers or miles do not apply. Our implied numbers could be called the Richter scale of planetary distance. Because distance measures space, I am calling this space logarithmic to differentiate it from ordinary space that we are accustomed to. By viewing these distances from a logarithmic perspective, the planetary distances become linear rather than exponential, In similar fashion, the Richter scale transformed the power of earthquakes into a more easily understood linear scale, i.e. 1 to 10, rather than 1 to 1010.
There is however a huge difference between the Richter scale and our logarithmic space. An earthquake’s power can fall anywhere on the Richter scale from 0 to 10, e.g. 2.4 or 6.7. In contrast, the orbital distances can only assume discrete, tightly defined values. With a simple conversion, we could construct a 1 to 10 Richter scale of orbital distances. In this case, both planets and moons must revolve at an integer distance from the central mass, whether Sun or outer planets. Put another way, these gravitational satellites do not inhabit the spaces in between these integer orbits. This discretization is our justification for referring to orbital distances as quantized, rather than continuous.
Orbits: Quantized Period
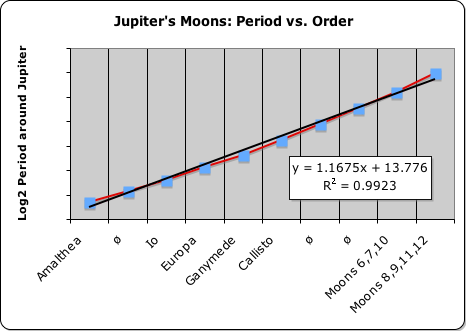
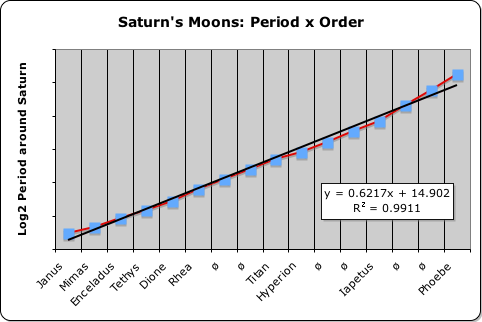
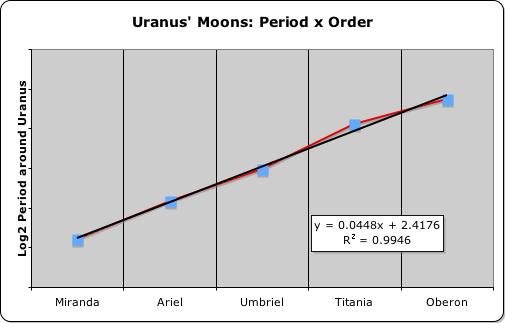
In addition to orbital distances, orbital periods are also quantized, as illustrated in the following four graphs. Again we plotted the log of an orbital dimension, in this case the orbit’s period, against planetary or lunar order in their respective systems. The first graph plots planetary order vs. the log of the planetary period. The subsequent graphs look at the moons of Jupiter, then Saturn, and finally Uranus in the same light: Period x Order.
In each of the four cases, we also calculated a correlation between the points and generated a best-fit line. The equation and correlation are shown in the highlighted box. Again the correlations are quite high, each above 99%.
We employed the same format with the Sun, Saturn and Uranus. In other words, we included the asteroid belt as a planet in the Sun’s system as before. In Saturn’s gravitational system, we inserted 6 phantom planets, indicated by ‘ø’, just like with the lunar distances. Uranus’ small system required no insertions as before. Jupiter was another story, as will be seen when we examine the chart.
In graphing Jupiter’s Moons: Period x Order, we inserted 3 phantom planets (ø) just like before. We then clumped Moons 6 & 7 for having similar periods, as before. This is where the similarity ends. Moon 8 is grouped with the outer moons, unlike before when it was grouped with Moons 6 and 7. More mysteriously, Moon 10 is totally out of order, as its period is shorter than Moons 8 and 9. We included it with the 6-7 clumping, as each of these 3 moons had similar orbital periods. Further we also grouped Moons 8, 9, 11 and 12 together as they also had similar periods. We justified this unusual organization because these outer moons are all moving in the opposite direction (retrograde) from the rest of Jupiter’s moons. (More on Jupiter’s unusual gravitational system when we examine orbital velocity.)
Orbits: Quantized Velocity
We’ve seen that both orbital distances and orbital periods are quantized. What about orbital velocities? Dividing distance by period produces the velocity. Just because orbital distances and periods are quantized, it does not necessarily follow that orbital velocities are also quantized. But they are, as the following graphs illustrate. Again the correlations between order and velocity are quite high: all over 98.5%.
We followed the same format as with the distance and periods: the Sun (1 phantom planet), Saturn (6 phantom planets) and Uranus (0 phantom planets). This time we completely excluded Jupiter’s last 4 moons from consideration. This position is somewhat justified in that Jupiter is now thought to have over 100 moons, not just the 12 we have included in our graphs. The Galilean moons, the ones Galileo viewed through his ordinary telescope, comprise over 99% of the lunar mass. The orbits of these major moons and some of the others are distinctly quantized, as our graphs illustrate.
Equation for Quantized Orbits Law
Our graphs have demonstrated fairly conclusively that the multiple orbits of planets or moons in spinning gravitational systems of our Sun are quantized with respect to distance, period and velocity. This fairly definitive conclusion was based upon the high correlation, generally over 99%, between Planetary/Lunar Order and the three aforementioned orbital features. Due to the presumed prevalence and relative certainty of this phenomenon, we have extravagantly deemed this the Quantized Orbits Law. Let us now write an equation that clearly exhibits the quantized nature of planetary and lunar orbits.
For each of our 12 Quantized Orbits Graphs, we generated a linear best-fit line. Its general appearance and equation is shown below.
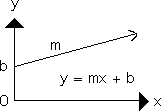
The x-axis in each of the graphs represents planetary order, while the y-axis represents the log of the chosen orbital feature, i.e. distance, period or velocity. The slope of the line is indicated by ‘m’ and the location where the line intercepts the y-axis is indicated by ‘b’. This is standard algebraic nomenclature.
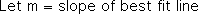
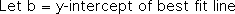
In the above equation, we can assign any real number to the variable x and determine the value of the variable y. In other words, the best-fit line is a continuous function. However in order to fit the quantized nature of our data, ‘x’ can only be a whole number (a positive integer) in the following equation. Due to this discretization, y can only be certain discrete step-like values, nothing in between. This is why the variable that represents three orbital features is quantized, rather than continuous.
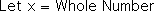
Employing the dimensions from our best fit line, the following equation represents a fairly good approximation of the empirical data from each of the graphs. Notice that our two equations, i.e. the best-fit line equation and the equation that matches the empirical data, are identical in every aspect but one. The variable x is restricted to whole numbers is the following, while it can be any number in the preceding.
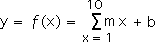
What is the relevance? By reversing the initial logarithmic process, we are able to convert y’s value into the standard dimensions one would find in a book of tables. In other words, if we raise 2 to the y power (2y), the result is a fairly good approximation of our empirical data regarding orbital distance, period and velocity. While far from perfect, it indicates that many orbital values are excluded from consideration, i.e. quantized.
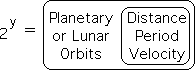
For this reason, we call it the Quantized Orbit Law – shown below. Capital Y is a variable that could represent the distance, period or velocity of the specified orbit. Y is solely a function of x, the order of the planet or moon from the large central mass in its gravitational system. As x can only be a positive integer, Y is quantized.
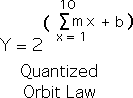
Mass, not a factor in function for quantized orbits
One more item of note: Although it is the masses of these gravitational systems that are ordered in such a precise fashion, mass is not a factor in our equation for quantized orbits. The amount of mass has no relationship to quantized distance, period or velocity. For instance, a planet’s distance from the Sun is primarily a function of its relative position relative to the other planets. This computation of distance does not rely upon mass. Although mass is ordered, it does not play a part in the computations. Intriguing to say the least.
Questions, Mysteries & Speculations
What are implications? Exponentially Expanded Space
What are the implications of the linear nature of these logarithmic orbits? Most of us believe and act as if the space that we inhabit is linear. The planetary orbits are spaced equally from a logarithmic perspective. Does this linearity suggest that the planets occupy a logarithmically condensed space from our perspective? Conversely, does this same regularity indicate that we occupy an exponentially expanded space from a planetary perspective? Does Einstein’s curved space explain this enigmatic feature of our solar system?
Equi-distant Rings? Nothing inbetween?
The equidistant rings are even more mysterious. Why is the distance between the planetary rings equal? Why doesn’t mass accumulate between each ring?
Parallel: Electron orbits: Discrete and Nothing inbetween
In order to understand this curious phenomenon, we look for parallels. The orbits of electrons within an atom provide us with an apt conceptual metaphor for understanding planetary orbits. Both planets and electrons occupy discrete rings about an exponentially heavier nucleus. Neither planets nor electrons ever occupy the spaces between the tightly defined rings.
Subatomic space quantized. Planetary Space quantized? Quantum Gravity?
The unoccupied space between electron orbits was a factor leading to the notion that subatomic space is quantized rather than continuous. Could planetary space also be quantized in some way? Does this provide evidence for quantum gravity? ? Or could there be another factor, perhaps an unknown force, that creates the discrete ridges that determine the location of the planetary orbits?
Parallel ends: Electrons jump orbits and give off or take in energy. Not planets
Unfortunately, this is where the parallels end between electron and planetary orbits. Identical electrons jump between energy levels – giving off and taking in energy, i.e. photons. Irregular planets never jump between orbits, nor do they give off energy. The electron orbits are not regularly spaced, while the planetary orbits are. While suggestive, the electron metaphor seems to be deficient in too many ways to provide much understanding.
Summary
It seems that Pythagoras was correct concerning the harmony of the planetary spheres. However, an understanding of the material cause behind this mysterious phenomenon is elusive at best.
The Titius-Bodes Law, Dermott’s Law & Planetary Resonance
Titius-Bodes Law
Although the word quantized has not been utilized, others have perceived the planetary harmonies. In 1766, Titius also noticed that the planetary orbits seemed to have a harmonic relationship with each other. After analyzing the data, he came up with a plausible hypothesis. Roughly speaking, Titius predicted that each planet in our solar system is twice as far away from the Sun as the preceding planet. As the one who wrote the mathematics, Bodes’ name is also on the so-called law.
The Titius-Bodes Law is a fairly good predictor for the solar distance of the visible planets. It also anticipated the orbital distance of both Uranus and even the Asteroid belt. However, it does not apply to Neptune’s or Pluto’s solar distance. Further, Titius did not incorporate either period or velocity into his speculations.
In 1968, Stanley Dermott came up with an empirical formula for the period of major satellites orbiting planets in our solar system. It is a more specific form of our formula for quantized orbits. In some way an extension of the Titius-Bodes Law, Dermott’s formula also lacks explanatory power and also does not address orbital velocities. Dermott does offer some speculations upon the whys behind quantization, but nothing definitive.
Planetary resonance provides an intriguing explanatory possibility for quantized orbits. It seems that the periods of planets will frequently naturally align with each other in distinct harmonic ratios, e.g. 1:2 or 2:4. However, this process is relatively unstable, i.e. not permanent. Planets drift in and out of resonance over relatively short astronomical time periods. As such, while suggestive, planetary resonance neither addresses quantized distances nor the stability and prevalence of the quantized orbits.
Summary
It seems that the velocity, distance, and period of planetary and lunar orbits are quantized. (Jupiter’s outer moons provide some notable exceptions.) Rather than a theory, this conclusion is instead a simple description of the orderly patterns of multiple sets of data. We graphed the orbital order of the planets and moons of the Sun, Jupiter, Saturn and Uranus against the logarithmic distances, periods and velocities of these same planets and moons. (4 gravitational systems x 3 orbital components = 12 graphs)
Each of the 12 graphs exhibits a high degree of linearity between the two sets of data associated with planetary and lunar orbits. The correlations are exceptionally high (over 98%). Although this type of quantization is prevalent in our solar system, it doesn't seem to apply to other gravitational systems throughout the galaxies.
Is it possible that the stable regularity of our highly ordered solar system enabled the origination of single cells? Could this stability have also provided the necessary preconditions for the tedious evolution of single cells into complex multi-cellular organisms like humans. If the quantized feature of our solar system is uncommon in the vast Cosmos, might Life only exist on Earth?
Thus far, this phenomenon lacks a broadly accepted explanation. Whether a feature of gravity or some other mysterious force, these quantized orbits indicate that we live in a highly ordered and resonant solar system – probably far surpassing the wildest imaginings of Pythagoras.