Section Headings
- Claude Shannon’s Information Theory
- Lehman’s Attention Theory
- Redundancy to achieve Exactitude
- Deduction’s Affinity with the Material Universe
- The Fragility of a Single Deductive Thread
- Numbers & Matter vs. Words & Life
- Life relies upon Redundancy Logic to determine Nature of Reality
- Academic & Scientific Redundancy Logic
- Summary
Synopsis
This article examines Information Theory (IT) from two vantage points: 1) as a mathematical system, and 2) as a unique form of logic. First, it compares and contrasts IT and Attention Theory as mathematical systems. The topics include the feature of reality that each applies to, their strengths and limits, and why they are complementary systems.
Second, the article suggests that IT’s Redundancy Logic (RL) is the primary form of logic that living systems employ to validate their hypotheses regarding the nature of reality. RL is necessary because Deduction’s power to draw Definitive Conclusions is dependent on Assumptions. While it is possible to make Definitive Assumptions in Mathematics and the Material Realm, it is virtually impossible in the Living Realm of Ideas and Behavior. As such, it is imperative that multiple types of the right type of cross-validation are employed to approach certainty regarding hypotheses and conclusions. Perhaps the best example is provided by Academia, which employs at least 5 different methods of redundancy to validate conclusions.
This article examines Information Theory from two vantage points: 1) as a mathematical system, and 2) as a unique form of logic. First, it compares and contrasts IT and our Theory of Attention as mathematical systems. The topics include the feature of reality that each applies to, their strengths and limits, and why they are complementary systems. Second, the article attempts to establish that IT’s Redundancy Logic is the primary form of logic that living systems including Academia employ to validate their hypotheses regarding the nature of reality.
Claude Shannon’s Information Theory
Claude Shannon initiated Information Theory in 1948 with his landmark paper – “A Mathematical Theory of Communication.” He proved that electronic transmissions could be as accurate as necessary if enough redundancy was employed in the code. The mathematically based Information Theory has enabled the miracles of our modern electronic devices. Because of Shannon’s theorems, we expect that the text, music, pictures, and movies that we send over the Internet are virtually identical on both sides of the transmission.
Shannon’s research: How to transmit Info between Machines
Shannon was employed to break and generate codes during World War II. During this time he learned about noise, codes, transmitters and receivers. After the war, Bell Telephone Laboratories utilized his talents to deal with the noise that interfered with their electronic transmissions from one location to another. The primary focus of Shannon’s research and theory was how to accurately transmit information from one machine to another machine.
Shannon only interested Machines & Information, not humans
People of that time obviously wanted their telephone calls and telegraph messages to be as accurate and noise free as possible. However, Shannon’s theories were not concerned with human behavior. He was only interested in machines and their relationship with Information. His theory has nothing to do with humans and their relationship with Information.
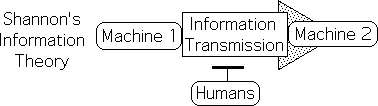
Shannon deliberately strips Info of Meaning
In order to solve this major engineering problem, Shannon deliberately stripped Information of meaning.
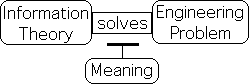
Meaning Irrelevant to Engineering Problem
He asserted accurately that meaning was irrelevant to his problem: the transmission of Information between machines. By disregarding the meaning that is so important to humans, he was able to develop the mathematical theory that is at the heart of our modern electronic wonderland.
“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem.” Claude Shannon 1.
IT’s Information is binary
Although he employs the common everyday word – information, he uses it in a purely technical sense. Shannon was only interested in Information that can be encoded into binary bits, 1s and 0s – the type used by machines. He defines Information in this manner, and even cautions his readers against projecting extraneous meaning onto the word or his theory.
“Information here, although related to the everyday meaning of the word, should not be confused with it.” Shannon2.
Simply put, the word blue has many connotative meanings to human beings. Possible meanings include the color of the sky or ocean or someone’s eyes or an even a sad emotional state. Yet Shannon is not interested in clarifying the meaning of the word blue in these contexts. Rather, he is interested in the clarity of the transmission of the word blue.
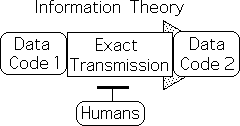
Virtually exact transmission possible
Shannon’s mathematics of binary strings inevitably proved that it was possible to achieve a virtually exact transmission of digital code from one place to another. In other words, there is a one-to-one correspondence between the electronic bits in the two machines. The content and order of the bits are preserved exactly. For instance, ‘blue’ is not transmitted as ‘bule’. There are no variations because no interpretations are required. Shannon is concerned with accurately replicating patterns that entail transmission.
IT does not address meaningful info
Shannon’s theory has nothing to do with the literary, auditory, and visual ‘information’ that we derive from our electronic devices. Digital code is certainly crucial to the clear production of the ‘information’ that brings us so much pleasure. However, Information Theory does not address this type of everyday ‘information’ because it is irrelevant to the engineering problem of transmitting strings of 1s and 0s.
AI attempt to apply IT to Humans
Because of the fabulous success of Information Theory regarding machines, Artificial Intelligence enthusiasts were and are quick to assume that humans also store, process and transmit information in a machine-like fashion, i.e. digitally. Indeed, they point to the supporting point that neurons are generally in an ‘on’ or ‘off’ position – a 1 or 0.
Unsuccessful for over 70 years
Due to these superficial correspondences, the adherents of AI assumed that Shannon’s supposedly universal principles would certainly apply to living systems. However in the 70 years since its inception, Information Theory has provided limited insight into Living Behavior or cognition. Despite many extravagant claims, it has provided little explanatory power with regards to Life’s relationship with Information.
Lehman’s Attention Theory
Information Theory, as mentioned, deliberately ignores our meaningful relationship with information. Attention Theory fills this gap. As such, the two theories could be considered complementary systems. Let’s examine their similarities and differences.
Both IT & AT based in mathematics of data streams
Information Theory (IT) and Attention Theory (AT) have a lot in common. Both theories are founded in mathematical systems that deal exclusively with data streams. In other words, the two systems belong to the same general set.
Material Mathematics, not in this set; No data streams, Matter ≠ Information
The Material Mathematics of Newton, Einstein and Feynman do not belong to this set. Data streams are not part of these systems. In addition, Matter is ultimately of a different nature and obeys different laws than does Information, either its technical digital definition or its more general sense as sensory data streams.
Mathematical Systems belongs to Greater Set: Similar constructs & architecture
However, each of these mathematical systems, i.e. those that deal with data streams and those that deal with matter, belong to a more general set. They employ many of the same mathematical constructs. For example, entropy is an important feature of each system. The constructs even belong to a similar architecture in each of the systems.
Information Theory > Machines; Attention Theory > Life
Despite belonging to the same set, Information Theory and Attention Theory have mutually exclusive components. On the most basic level, Information Theory only applies to machines, while Attention Theory only applies to Life. This is but one way in which the two theories are complementary.
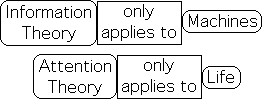
IT binary strings for Machines; AT sensory data streams for Life
While both systems deal with data that comes in discrete chunks, i.e. data streams, the data contained in the respective streams is quite different. Information Theory specializes in the binary strings that are exclusive to machines. Attention Theory specializes in the sensory data streams that are exclusive to living systems.
Attention Theory: Meaning a prime focus; Information Theory ignores
While Shannon’s work ignored the human relationship with Information, a prime focus of Attention Theory is how humans derive meaning from Information. Specifically, how do we make meaning from sensory input? We rely upon engineers to ensure that our electronic transmissions are accurate – text messages, pictures, and music. But how do we make sense of the sensory input we get from our machines, e.g. CDs, DVDs, cell phones and screens?
AT proposes a computational method for extracting Meaning from DS
Information Theory ensures the accuracy of the transmission from one machine to another. At this point, humans enter the story. After reading the text, listening to the music, or seeing the pictures, we attribute meaning to the message. In other words, our machines generate a digitally based transmission that is accessible to our senses. While Information Theory is deliberately mute about meaning, Attention Theory proposes a computational method that we could employ to derive dynamic meaning from sensory input.
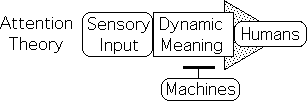
AT based in LA, which generates DSD, the source of Dynamic Meaning
Attention Theory is based in the Living Algorithm (LA). The LA generates a mathematical system deemed Data Stream Dynamics (DSD). One of the propositions of Attention Theory is that living systems employ the LA as a computational interface to extract dynamic meaning from Data Streams.
![]()
LA processes Information, sensory data streams, & relative Info
The LA is able to process a larger set of data streams than the mathematics of Information Theory. While Information Theory is confined to digital Information, the LA can deal with Information that comes in almost any form, e.g. digital, sensory, and conceptual. Rather than always digital, the data can also be of a relative nature, e.g. ‘greater than’, ‘much greater’ ‘towards the right’, ‘in the middle’.
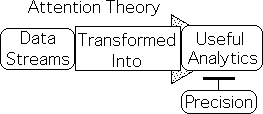
LA sacrifices exactitude for useful analytics, IT exact
Information Theory enables a virtually exact one-to-one correspondence between the electronic data that is transmitted and received between two machines. While we expect exactitude from machines, humans, in fact all living systems, need ongoing analytics that facilitate better probabilistic predictions. The LA serves that function. The mathematics immediately transforms data streams, sensory or otherwise, into ongoing analytics that could be useful to any living system. However, the exactitude of the data is sacrificed for meaningful analytics.
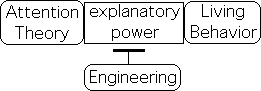
AT provides explanatory power regarding Living Behavior, IT none
While Information Theory solved an engineering problem but ignored humans, Attention Theory provides a great deal of explanatory power regarding human behavior, but has no engineering applications. The first deals with the relationship between machines and Information, while the latter focuses upon the relationship between living systems and sensory data streams. Information Theory addresses machines and electronic transmission. Attention Theory addresses the relationship between Attention and our senses.
AT & IT complementary
It is evident that Attention Theory and Information Theory are complementary systems. They are both based in mathematical systems that specialize in data streams. Yet IT specializes in machines and exact transmissions without meaning, while AT specializes in living systems, useful analytics and dynamic meaning.
Redundancy to achieve Exactitude
IT: Exactitude attained via code Redundancy
Information Theory is interesting for yet another reason. In addition to solving a major engineering problem, Shannon also introduced a new type of logic – redundancy logic. He employed this type of logic in a deductive fashion to achieve a virtually exact transmission of coded Information from one machine to another.
“It was Shannon’s achievement, in his 1948 papers, to show that in any type of communications system, a message can be sent from one place to another even under noisy conditions, and be as free from error as we care to make it, as long as it is coded in the proper way. Nature does impose a limit, but the limit is in the form of the capacity of the communications channel. As long as the channel is not overloaded, then the code guarantees as high a degree of accuracy as we choose. Shannon proved that such codes must exist in the most famous of all this theorems.
Shannon’s Second Theorem
It is usually known simply as Shannon’s second theorem, and was one the major intellectual discoveries of the time, because it seemed to run counter to common sense. By showing that reliable information is possible in an unreliable world, the second theorem has the status of a universal principle, because ‘information,‘ as defined in a new way, is universal. It is an aspect of life itself, not merely communications engineering.
Error-correcting codes may need to be extraordinarily ingenious, but, in principle, they can insure perfection in the midst of imperfection, order in the face of disorder, by adding redundancy of exactly the right kind.” 3.
Shannon’s second theorem proved that virtually exact data transmission is possible from machine to machine. With enough code, engineers can obtain any level of accuracy that might be desired. These error-correcting codes are based in redundancy.
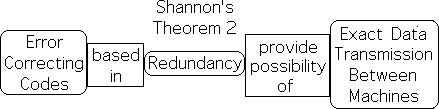
Most Powerful Form of Logic for Living Systems
Despite employing redundancy to achieve accuracy, Shannon didn’t name his logical method, as he probably considered it a form of deduction. Nor did he realize the implications of his technique. While Shannon only applied this type of logic to machines, I am suggesting that Redundancy Logic is the primary form of logic that living systems including Academia employ to determine truth in our uncertain world. As we shall see, the academic community actually utilizes five different types of redundancy to validate their hypotheses regarding the nature of reality.
Redundancy: Negative Connotations, boringly repetitive
These ideas might seem bizarre as redundancy frequently has a negative connotation. It usually means too much repetition. When teachers wrote this word on our papers, it meant delete a word, sentence, or even paragraph. A long-winded, boring talk or article is considered redundant when it repeats the same information in the same way too many times.
Redundancy useful: Shift exchange example to avoid misunderstanding
However, redundancy also serves many useful functions. To better understand the positive applications, here is a simple example of verbal redundancy. Servers, where I work, employ texting to rearrange our schedules. For instance, I might want someone to cover my shift if an old friend shows up unexpectedly. To avoid potential ambiguity or misunderstanding, my text might include both day of the week and date, e.g. Tuesday March 3. Without the date, the recipient might assume the wrong week. The recipient must then text the manager of the schedule change to validate that she has agreed. Rather than a boring flaw, these redundancies act as forms of cross validation. They ensure that my fellow server has agreed to and will show up to work on the correct evening and cover my shift.
Binary transmissions: Redundancy detects error: Change from 0 to 1
Shannon’s redundancy is based in a more sophisticated form of cross-validation. Machine transmissions, along with the error-correcting codes, are written in a binary form. Validating the transmission via redundancy detects when code is wrong. If it is 0, then the code is simply changed to 1. Problem solved.
Error-correcting codes may contain more bits than Message
If the transmission has the potential to be quite noisy, the error-correcting codes might contain more bits of Information than the message itself. For instance in space travel, the redundancy codes sometimes contained up to 15 times as many bits as the desired information. This disparity reflects both the importance of the information and the distance traveled.
Deduction’s Affinity with the Material Universe
It is evident that redundancy enables the accuracy of our electronic transmissions. But Redundancy Logic (RL)? Why is it even necessary? Isn’t redundancy is just another form of Deductive Logic? That was certainly Shannon’s conception of his method. Aren’t the other forms of logic enough? What differentiates RL from the rest?
Induction, a form of Pattern Recognition, can’t make Definitive Conclusions
We are generally taught that there are two types of logic: deduction and induction. Induction is a form of pattern recognition. We induce general patterns from specific examples. Inductive logic cannot be employed to reach definitive conclusions.
Deduction, most Powerful form of Logic, because leads to necessary conclusions
In contrast, Deduction operates on general assumptions to reach necessary conclusions. ‘Necessary conclusions’ is a way of saying that these conclusions are always true, at least if the assumptions are true. Because Deduction leads to definitive truth, it is generally considered to be the more powerful of the two types of logic.
Deduction validates Induction’s Conclusions
As an example of this power, Deduction is required to validate Induction’s conclusions – not vice versa. Indeed mathematicians employ a deductive technique to affirm the numerical patterns that are reached through induction. They must prove deductively that an individual example and the general statement are both true. Both proofs must be included to validate the pattern. Similarly in expository writing, generalizations typically require the support of specific examples.
Deduction & Induction, the standards: What need for Redundancy?
If Deduction is so powerful, why is there a need for another type of logic? A brief historical narrative will assist us to better understand both the power and the limitations of the notion that deduction is the most powerful form of logic.
Euclid’s Geometry:
During the Renaissance, European thinkers became aware of Euclid’s Elements. Euclid begins with some seemingly simple assumptions. He employs deductive logic upon these assumptions to generate theorems and corollaries. The extension of these basic theorems generates the entire mathematics of geometry. This straightforward book had and continues to have an overwhelming influence upon Western thought.
Deduction: Logic of Necessity
The conclusions of deductive reasoning follow of necessity from clearly delineated assumptions. There is no ambiguity or subjectivity involved. The geometric conclusions arrived at by ancient Greek mathematicians are true at all times and in all places.
Deductive Reasoning: the foundation of Objective Mathematics
Deductive reasoning is the foundation of mathematics. If the logic is sound, mathematical conclusions are always true. There is no subjectivity; no cultural relativism; no ambiguity. Although there is an incredible diversity of beliefs, all reasonable humans, regardless of race, religion, culture, or sexual persuasion, recognize that the deductive conclusions of mathematics are objectively true.
Math addresses an Ideal, not Real, World
Math’s perfect truths have a significant problem. Mathematical certainty is based upon an ideal world, rather than our fuzzy reality. However the ideal world of mathematics does seem to apply to many of the ambiguities of the real world.
Math’s deductive Logic applies to Material World
The Pythagoreans of ancient Greece were probably the first to assert that Math does apply to reality. Euclid’s geometry certainly applies to static objects and areas. Arab mathematicians extended this understanding to architecture. Then to everyone’s surprise and amazement, Galileo’s experiments revealed that mathematics also applies to the dynamics of matter.
From static to dynamic world & then modern science
Prior to this point, math had only been applied to our static world. This discovery illustrated that our dynamic world was also under the sway of mathematics. It was at this point in history that modern science was born.
Functionally exact fit between Math & Material Dynamics
As time passed, scientists discovered that the fit between mathematics and material dynamics is functionally exact. Countless experiments and inventions have repeatedly pointed to the same conclusion. The technological miracles of our modern world are a mute testament to the exactness of the fit. Due to this perfect match, mathematics with its deductive logic has acquired an almost divine status.
Contrast: Objective Mathematical Logic & Subjective Religious Beliefs
It is certainly amazing that the unambiguous certainty and objectivity of deductive Mathematics can be effectively applied to the seemingly imprecise and ambiguous world of Matter. This happy marriage of mathematical truth and empirical reality was and is appealing, even intoxicating, to philosophers and scientists then and now. The absolute and unassailable deductive truths of mathematics stand in stark contrast to the subjectivity of personal opinion, superstitious beliefs and religious dogma.
Philosophers: “Let’s apply deductive logic to philosophy.”
This dichotomy between objective science and subjective beliefs inspired many attempts to apply the unquestionable certainty of deductive logic to the human realm. Philosophers thought, “Let us employ deductive reasoning to clean up the messy world of religion.”
Can the deductive reasoning of mathematics really be applied to philosophy and the world of thought?
Descartes’ Euclidean Philosophy
Descartes, the philosopher and mathematician, was probably the first to attempt to employ Euclid’s deductive structure to organize philosophy and by extension human thoughts and beliefs. With his famous statement – “I think, therefore I am,” he believed that he was establishing a first principle, i.e. an assumption, upon which he could apply deduction to arrive at necessary conclusions. Thoughts, of course, are a feature of the living world. While engineers can effectively apply precise mathematical formulas derived through deductive reasoning to manipulate the material world, living behavior is tricky.
Philosophy resists Deductive Reasoning
While influential, Descartes’ attempt to Euclidize philosophy never attained the absolute truth of Euclid’s Elements, and by extension mathematics. Indeed many philosophers, e.g. Spinoza, have attempted to apply Euclid’s logical structure to human beliefs. These efforts continued for over three centuries – well into the 20th century. None of these attempts have been successful at establishing universally accepted truths. While deductive reasoning generates the absolute truths of mathematics, this same type of definitive logic seems to be helpless before human thought.
Just as philosophers attempted to apply deduction to ideas, scientists have tried to apply deduction to Living Behavior. After all, they had uncovered deductive mathematical formulas that mirrored Material Behavior. If Life consists solely of Matter, then it should be possible to uncover mathematical formulas that accurately reflect Living Behavior. However, the quest to employ deduction to make definitive conclusions regarding Living Behavior has also been unsuccessful.
Why?
The failure to establish universal truths by employing deductive logic was certainly a disappointment to many thinkers and scientists. Why is the deductive approach to beliefs and living behavior generally unsuccessful? To find out, let’s first examine the limitations of deductive logic.
The Fragility of a Single Deductive Thread
Deduction: Logic of Math, Matter, & Technology
Deduction is obviously a powerful form of logic. It is the foundation of Mathematics, which can predict Material Behavior almost perfectly. This amazing correspondence has resulted in our equally amazing modern technology. In brief, Deduction provides the logical foundation for Mathematics, Matter and Technology.
Deduction: No Definitive Conclusions regarding Ideas & Living Behavior
This impressive array has imbued Deduction with well-deserved prestige. It is easy to see why philosophers would attempt to apply this same logical system to beliefs to attain truth and scientists would attempt to apply it to living behavior to make definitive predictions. Yet despite centuries of sincere attempts by many brilliant minds, Deduction has not resulted in any necessary (absolute) conclusions regarding Philosophy and Living Behavior.
Why?
Why? What’s the problem? Is an insight just around the corner? Or are there some innate limitations to Deduction? To come to a better understanding of the difficulties, let us examine the deductive process in more detail.
Process: Deduction -> Assumptions -> Necessary Conclusions
The logical process is straightforward. Deduction operates upon Assumptions to reach necessary (definitive) conclusions. There are several features of this process that bear examination.
Deduction -> Assumptions -> Necessary Conclusions
Definitive Assumptions -. Definitive Conclusions
First, in order to reach Definitive Conclusions, the Assumptions must be equally definitive. Ambiguous Assumptions result in Ambiguous Conclusions. For Deduction to attain certainty, the Assumptions must be absolutely clear. Anything less results in imprecision.
Definitive Assumptions -> Definitive Conclusions
Ambiguous Assumptions -> Ambiguous Conclusions
Assumptions determine Truth, not Logic
The Deductive process has yet more limitations. The Assumptions determine the nature of the Conclusions, not the Logic. If the Assumptions are definitive yet questionable, Deduction can easily come up with questionable, perhaps even what most consider to be false, conclusions. Further, if the assumptions are different, then the conclusions will be different, maybe even contradictory. To better understand, let’s look at a mathematical example.
Questionable Assumptions -> Questionable Conclusions
Different Assumptions -> Different (even Opposite) Conclusions
Lobachevsky: Different Assumption than Euclid à Different Geometry
For centuries, if not millennia, philosophers believed that Logos or logic determined the Truth. Euclid’s Elements provided an excellent example that supported this assumption, or so it seemed. Then in the early 1800s, Lobachevsky did something very controversial. He challenged this widespread paradigm by starting with a slightly different assumption regarding parallel lines than did Euclid. He employed deduction upon this new assumption and generated an entirely new form of geometry. The two forms of geometry employ deductive logic to arrive at contradictory conclusions. For instance, triangles have exactly 180º in Euclidean geometry, while they have less than 180º in Lobachevsky’s geometry.
Euclid: Flat Planes; Lobachevkey: Curved Space
Which is true? Even though they consist of conflicting conclusions, both mathematical systems are equally true. It turns out that each type of geometry has a different application. Roughly speaking, Euclid’s geometry applies to flat planes, while Lobachevsky’s geometry applies to curved space. This Non-Euclidean version is not just a mathematical curiosity, as many claimed. Einstein used curved space geometry to derive some of his theories.
Redundancy of Empirical Data to determine Context of Mathematical Truth
To determine which type of geometrical system is applicable in a given situation, empirical data must be taken into account. It requires the redundancy of empirical data to establish the system’s truth regarding our reality. And this is in the Material Realm. The Living Realm is far more complex.
Alfred Tarski: Proves that Logic can’t determine Truth
Despite this mathematical example, philosophers and logicians continued to hold onto the notion that logic could be employed to arrive at absolute truth. Then in 1933, Alfred Tarski published a theorem that shattered these misguided hopes. Based in self-referential constructions, Tarski’s Theorem essentially proves that Logic can’t determine Truth.
Assumptions determine Truth and Falsehood, Not Deductive Logic
The Assumptions determine Truth and Falsehood, not Deductive Logic. We can employ logic to suggest plausible Assumptions or challenge Assumptions. Yet Deduction’s Conclusions are inevitably dependent upon the Assumptions.
Examples of Assumptions in Human Realm that lead to Different Conclusions
Here are just a few rough examples of assumptions that are made in the Human Realm. Each of these groups operates upon the assumption that their specific category is the most important. Each applies deduction to this assumption to arrive at wildly different conclusions.
Science: Empirical Data
Religion: Beliefs
Fascism: Nation
Liberal Democracy: Individual rights
Social Democracy: Collective rights
Christian Assumptions -> Evolution False
For example, many Christians start with the assumption that the Bible is the Word of God. If this is so, then the World was created in 7 days. If the World was created in 7 days, then Geology, Dinosaurs and Evolution are False. Pure Deduction.
Scientific Assumption -> Evolution True
Scientists start with the assumption that Truth must be based upon Empirical Data. Under this assumption, Geology, Dinosaurs and Evolution are all True. Even though Deduction is applied in both cases, the Conclusions are diametrically opposed.
How to determine which is True?
If Deduction results in contradictions, how is it possible to determine which conclusions are true? Do we throw up our hands in despair and adopt a position of absolute moral relativism? Or is there another logical method for ascertaining truth?
Summary of Deduction’s Limitations
While an incredibly powerful form of logic, Deduction has some distinct limitations. The power of Deductive Logic is dependent upon nature of the Assumptions. While Definitive Assumptions result in Definitive Conclusions, Ambiguous, Questionable, and/or Differing Assumptions lead to equally Ambiguous, Questionable, and/or Differing Conclusions.
Deduction fragile due to fragility of Assumptions
Ultimately the strength and nature of the Assumptions determine the strength and nature of the Deductive Conclusions. Put another way, Fragile Assumptions result in Fragile Conclusions.
Strength of Assumptions -> Strength of Conclusions
Fragile Assumptions -> Fragile Conclusions
Is there any resolution to the fragility of Deduction’s logical chains?
Numbers & Matter vs. Words & Life
Deduction works so well with Math, Matter and Technology. Why have so many great thinkers had such difficulties applying this powerful form of logic to Philosophy and Living Behavior? Could it be that Words and Life have some innate features that undermine the use of deductive logic? To provide context, let’s first explore why Mathematics and Matter are so susceptible to Deduction’s charms.
Numerical epitomize Absolute essence
Numbers and symbols are the letters of the language of Mathematics. These symbols have rigorous definitions that identify absolute numerical essence. The elements of the Assumptions that Deduction operates upon to draw Definitive Conclusions must have an absolute essence – either inside or outside the box. Deduction can be applied to absolute numerical essences to arrive at equations that are either true or false. No ambiguity – no shades of grey – no subjectivity. By operating upon absolute numerical essences, deduction generates the absolute truths of mathematics.
Consisting of absolute essences, Material world subject to Deductive Mathematics
Scientists have discovered that the material world also consists of absolute essences, e.g. atoms, molecules, electrons and photons. A major focus of the material sciences is to derive equations that match the behavior of absolute numerical essences with absolute material essences. In such a way, they are able to apply deduction to both matter and mathematics to come up with necessary conclusions, read absolute truths. With the proper initial conditions and the correct equation, they are able to make the perfect predictions that are the basis of our technological wonderland.
Avogadro’s Number
Let us offer a few concrete examples from the Material Realm. Avogadro discovered that equal volumes of all gases with the same pressure and temperature also have the same number of molecules. Further, his name is associated with the number of molecules in a set quantity – 6.02 x 1023. Adding but one of these exceptionally tiny molecules to the gas will change for instance the temperature by a tiny yet predictable amount – every time in all places and time periods.
Pauli’s Exclusion Principle
How about the Subatomic Realm? Pauli’s Exclusion Principle holds that subatomic particles of the same kind are indistinguishable and only one can occupy a specific quantum state at a time. Affirmed so many times, this principle is considered to be a law. Evidently in both the Molecular and Subatomic Realms, classes of identical particles behave identically in all times and places. In the Material Realm at least, absolute laws characterize the absolute behavior of absolute essences.
Words: Innate ambiguity due to infinite regression of definitions
What about the Living Realm? In contrast to Numbers, Words have some innate ambiguity to their meaning. This is due in part to the imprecision of understanding between transmitter and receiver. Further, words themselves can only be defined with other ambiguous words. This leads to an infinite regression of imprecision.
Tarski: theoretical primitives
Tarski also proved that theoretical primitives are at the basis of every deductive system. Theoretical primitives are concepts or assumptions that can’t be precisely defined without relying upon other theoretical primitives – an infinite regression of definitions. As they resist definition, their meaning is only established by appealing to intuition and/or experience. Even the most rigorous of systems has some intuitive or experiential ambiguity at its base. This introduces an element of uncertainty.
Deduction can’t be applied to words/beliefs to determine truth
Due this ambiguity, non-numerical words can’t be treated as absolute essences. Because deductive logic requires absolute essences to perform its magic, deduction can’t be applied to words, and by extension beliefs, to arrive at necessary conclusions. The innate ambiguity of words is one reason that philosophers have not been able apply deduction to assumptions to determine truth.
Example: Descartes’ Mind/Body Duality
Descartes’ Mind/Body Duality provides us with a good example of the problem. Mind continues to have many debatable meanings even among academics. Because of the continuing ambiguity of Mind, i.e. its resistance to a universally agreed upon definition, deduction can only reach ambiguous conclusions on this topic. It can’t be employed in the same fashion that Euclid did when he created the immutable laws of geometry.
Living Behavior resists Deduction
Living Behavior is also resistant to the inescapable conclusions of deductive logic. Many reputable scientists have attempted to apply deduction to first principles to arrive at necessary conclusions regarding human behavior. Yet there are still no equations that can make definitive predictions regarding the behavior of even a single cell, much less humans.
Cells in a constant Flux, no absolute Essence
Why does deduction have such a problem drawing definitive conclusions regarding living systems? While the content and behavior of every electron is identical, the content and behavior of every cell, the building blocks of Life, is different. First, individual atoms and molecules are coming and going from living systems at all times. Second, the internal structure of every organism and organelle is in a constant state of flux in the attempt to maintain homeostasis. Unlike atomic and subatomic particles, cells do not have an absolute content.
Matter: Reactive; Life: Interactive Feedback Loops
Further Material Behavior is reactive; while Living Behavior is interactive. Matter’s reactive nature obeys the predictable deductive chains of set-based mathematics. Life’s innate nature consists of interactive feedback loops that do not adhere to the absolute certainty of set-based mathematics. Due to this innate feature, Deduction cannot be employed to make definitive statements regarding the behavior of living systems. (We deal with this topic in more depth in another article: Matter’s Regular Equations vs. Life’s Disobedient Equations.)
Definitive Assumptions possible in Math & Matter, not Beliefs & Living Behavior
It is possible to make the Definitive Numerical and Material Assumptions that are at the foundation of Mathematics and the Material Sciences. It is difficult, if not impossible, to make Definitive Assumptions regards Beliefs and Living Behavior. Due to this difficulty, Deduction has distinct limitations in the Living Realm. Is there any resolution to this logical conundrum?
Life relies upon Redundancy Logic to determine Nature of Reality
Deduction can’t reach necessary conclusions regarding verbal concepts or Living Behavior. The innate ambiguity of words and Life’s interactive feedback loops prevent the formation of definitive assumptions. It is evident that this powerful form of logic has many limitations regarding both Words and Living Behavior. Is it possible that Redundancy Logic could effectively transcend these limitations?
Single Code/Logical Chain Insufficient; Multiple Codes/Logical Chains required
Shannon’s Second Theorem proves that engineers can approach an exact transmission of Information by adding the right type of redundancy into the code. In similar fashion, redundancy’s cross-validation enables living systems to approach truth regarding the nature of reality. Just as a single code is generally insufficient for achieving exactitude, a single logical chain is unable to establish truth with any certainty. Just as multiple layers of code are required to approach exactitude, multiple layers of the right kind of redundancy are required to establish a higher degree of certainty.
Living Systems: Multiple Senses evolved to provide redundant cross-validation
Let’s look at some examples.
Living Systems employ redundancy as the prevalent form of logic. On the most basic level, our senses evolved to provide cross-validation. We hear a loud noise and then look to see what caused it. The predator/prey dynamic includes smell, sound, sight, touch and hopefully taste for the predator. Those creatures with the best senses tended to be the most successful at procuring a meal or avoiding becoming one. A single sense is not enough in and of itself to reach a definitive conclusion. The redundancy of multiple senses enables us to hone in upon certainty. Was I just hearing the wind, or could it have been an intruder?
Social Interactions require Redundancy
Our social interactions provide another salient example. We see a person’s appearance, listen to his sounds, shake his hand or hug his body to better assess his intentions. During the interaction, we attend closely to facial expressions, voice nuances, meanings of spoken words, and behaviors to know what to expect and respond appropriately. If the interaction is important enough, we might even consult other humans as a character reference. These are all forms of redundant cross-referencing.
Relying upon only one source results in being Deceived
Indeed those humans that only rely upon sight and words are frequently deceived, both interpersonally and politically. Relying exclusively upon our vision to determine the truth is similar to relying upon a single thread of deductive logic. As the expression goes, sometimes appearances are deceiving. Instead of just one sense, most of us employ multiple senses to gain a better understanding of the nature of reality
Verbal Interactions: True-False Theorem
We also employ redundancy logic in our verbal interactions. Due to the innate ambiguity of words, both their definitions and the Speaker/Listener problem, statements have both a true and false component. The Listener attempts to discern what is true and what is false. The only way to discern what the Speaker really means is via redundancy. The Listener might ask clarifying questions or the Speaker might say the same thing in another way or perhaps provides examples. These redundancies enable the Listener to hone in on the truth, i.e. what the speaker really means.
Literature: Best writers convey the same concept in many ways
Literature provides us with yet another example. It is easy to misinterpret intention and meaning with only a single source. The best authors have multiple ways of using redundancy. They employ multiple words for the same concept, express the same concept in many different ways, and illustrate their paper or book with diagrams, graphs and pictures. Indeed we are taught to tell the reader what we are going to say, say it, and then tell them what we have said. With all this redundancy, the reader is less likely to go astray and is better able understand and remember the author’s true meaning.
Redundancy of Examples to support Proposition that Humans employ Redundancy
Multiple Senses provide redundancy to better ascertain the nature of reality. Our social interactions, speech and literature are filled with redundancy to better assure the accuracy of the meaning of the message. These four broad examples act as a form of redundancy to support the proposition that humans rely upon Redundancy Logic to hone in on the truth. Following is yet another example that creates an even deeper weave for our Redundancy Fabric.
Academic & Scientific Redundancy Logic
Academia requires Multiple Forms of Redundancy
Each of us, indeed all living systems, employ redundancy frequently everyday to better understand the meaning of sensory input, social interactions, and the transmission of ideas. However, Academia has taken Redundancy Logic to a higher level.
Redundancy Logical Fabric basis of Academic Truth
This esteemed community doesn’t just hope for or intuitively rely upon redundancy to suggest meaning. Multiple forms of redundancy must point in the same direction before the academic community accepts the conclusions. I think it is even safe to say that, redundancy provides the logical fabric that determines scientific and scholarly truth.
![]()
Academia: 5 types of Redundancy
Just as engineers employ multiple forms of code redundancy to approach exact transmission, Academia also employs multiple forms of redundancy to establish the validity of their conclusions. These forms of redundancy can be broken into 5 categories: 1) logical chains, 2) collective consensus, 3) empirical evidence, 4) experimentation and 5) mathematics, preferably a system.
1) Deduction & Induction threads of Redundancy Fabric
1) Logical Chains. Deduction, induction and correspondence provide the logical threads that create the fabric of redundancy logic. Rather than just a single, fragile logical thread, academia requires multiple logical chains of varying types to validate conclusions.
2) Collective Consensus Redundancy: Academic Journals
2) Collective Consensus. Journals provide a great example of this form of redundancy. Scholarly and scientific articles are filled with footnotes that reference relevant articles that support their position. This cross-referencing provides the cross-validation that strengthens their claim. With enough redundancy of this nature, the claim could even become a widely accepted theory or scientific fact.
Global cross-generational consensus
Rather than merely localized or contemporary, journals establish a global cross-generational consensus regarding relevance and conclusions. A professor’s theories die when his followers, i.e. graduate students, fail to convince the next generation of its veracity or relevance. Perhaps a bigger narrative replaces a smaller narrative in the ongoing data stream of journal articles. Indeed one point of this article is to convince the reader that Redundancy Logic belongs to a bigger narrative, as it is a more all encompassing form of logic than Deduction and Induction.
3) Empirical Evidence
3) Empirical Evidence. Science, in particular, requires empirical evidence as a form of redundancy.
Galileo challenges Beliefs & Logic with Empirical Evidence
Galileo probably initiated this requirement. To test the validity of Medieval Beliefs and Aristotelian Logic, he performed some experiments and made some visual observations. After dropping balls of differing weights from the Leaning Tower of Pisa, he observed that they all landed at the same time, thus confuting Aristotle’s Logic that heavier balls fall faster. Employing a telescope, he saw moons circling Jupiter, thus confuting the prevalent belief that the Earth was the center of existence. Galileo conclusively illustrated that Logic and Beliefs are not sufficient in and of themselves to determine the nature of reality. They must be supported by evidence.
Redundancy of Better Measurements initiates Theory changes
There are many types of empirical data. Generally speaking, the theories of the Material Sciences are based upon exact evidence. This is because scientists can produce relatively precise measurements regarding their prime components, e.g. distance, time and mass. The redundancy of ever better measurements has even resulted in significant theoretical changes. Kepler’s elliptical orbits and Einstein’s relativity theory both came about due to more precise data.
Dr. C’s Flow experiments take Evidence Redundancy to new level.
Due to the innate ambiguity of their focus, Living Sciences must be satisfied with less exact measurements. Psychology is known for their endless questionnaires combined with crosschecking statistics as a form of redundancy. Dr. C., the originator of Flow Theory, took Redundancy to a new level with regards evidence.
Subjective Evidence, i.e. Personal Perception, fatally flawed
His evidence was controversial. His subjects were asked how happy they were at different times during a week. Rather than objective measurements, Dr. C’s conclusions were based upon notoriously subjective personal perceptions. His individual evidence, i.e. self-reported states of happiness, was questionable at best.
Dual Redundancy: Huge sample size + Consistent results
To get around this problem, Dr. C added two levels of redundancy. First, rather than a small sample size, which would have been doomed from the get-go, he took millions of global readings. This level of redundancy was supported by consistent results. Academia finally accepted his conclusions and theory due to the dual redundancy of consistency combined with sheer numbers. Kahneman refined Dr. C’s theories by adding another layer of questioning, yet more redundancy.
4) Experimentation: Rules behind designed to produce Best Evidence
4) Experimentation provides yet another example of the necessity of scientific redundancy. Experiments are designed to produce the best evidence possible. There are tightly defined rules of procedure, another form of redundancy, to ensure that the evidence is of the highest quality. The academic community at large then questions each point of procedure, the assumptions and the conclusions.
Single Experiment requires Replication, Multiples, Cross-Disciplinary
Yet, one experiment, no matter how good the design, is not enough to determine scientific truth. A single experiment is just as fragile as a single deductive chain. On the first level, the experiment requires replication. On the second level, multiple experiments must point in the same direction. Finally, if a hypothesis gains cross-disciplinary validation, it becomes a generally recognized scientific theory. Deduction can operate on these first principles to arrive at necessary conclusions. But Science requires that even these definitive conclusions be supported by empirical data.
5) Mathematics-Data Synergy reveals Logic Structure
5) Mathematics is also a form of redundancy. By itself, it is an imaginative abstraction with no ties to reality. However, sometimes a mathematical system is linked with patterns of Empirical Evidence. As mathematics is based in deduction, the system can reveal the underlying logical structure of this feature of reality. This is a powerful form of Redundancy as it connects deduction with evidence. When there is a Math-Data Synergy of this nature, the assumptions that underlie the Mathematical System are generally considered to be true.
Notable Math-Data Synergies
Following are several examples of some notable Math-Data Synergies. The list begins with the inventor of the mathematical system and follows with the feature of reality that the mathematics applies to.
Newton: Material Dynamics
Einstein: Relativistic Conditions (Extreme)
Feynman: Subatomic Dynamics
Shannon: Information transmission between Machines
Lehman’s Data Stream Dynamics: Rhythms of Attention
Math-Data Synergy requires incredible amount of redundancy
An incredible amount of redundancy is involved in these Math-Data Synergies: the logical chains, the mathematical fit, the empirical evidence, the experimental design, and the academic consensus.
Attention Theory flawed without Academic Consensus
I jokingly added my Attention Theory to the bottom of the list. As of yet, this personal entry is flawed in that Academia is unaware of its existence. The academic community has not yet crosschecked the logic, the mathematics, the empirical evidence and the conclusions. Without this redundant validation, the entire project is doomed to obscurity and will fade with my death.
New Theory especially requires Redundancy: Wegener’s Continental Drift
When a new theory contradicts the current paradigm, it especially requires the cross-validation of Redundancy Logic. The theory of plate tectonics provides an excellent example of this phenomenon. In 1915, Alfred Wegener published a book in which developed his hypothesis of continental drift. He supported his hypothesis with an abundance of evidence. Both the flora and fauna in Africa and South America had undeniable similarities. Further the coastlines of the two continents fit together like two pieces of a gigantic jigsaw puzzle.
Wegener’s Continental Drift rejected as violates fixed Earth Paradigm
However the scientific community rejected his hypothesis because it contradicted the common sense logic of the fixed earth paradigm. How could continents move and why would they break apart from each other? Wegner actually became a laughing stock along with his moving continents hypothesis.
Accepted as Plate Tectonics due Interdisciplinary Cross-validation: Redundancy
It was only decades later that the continental drift hypothesis was validated and morphed into theory of plate tectonics. This acceptance of Wegener’s paradigm busting position was due to the redundancy of interdisciplinary cross-validation. Incontrovertible evidence from multiple disciplines both affirmed the hypothesis and provided a mechanism for movement. The evidence included the alignment of geo-magnetic fields and a spreading ocean. Due to the logical redundancy from so many fields, plate tectonics theory is considered to be an indisputable scientific fact.
Redundancy Logic validates Theory of Attention
By linking a mathematical system to Choice, Mental Energy, and Life, the Theory of Attention also violates the current paradigm. As such, it requires abundant redundancy of the right type to establish its validity. That is the purpose of this book. It began with some logical reasons why Life might employ the LA as a computational interface to assign meaning to the info contained in data streams. The following chapter illustrated that there is a strong connection between the LA’s Pulse and Sustained Attention Experiences, a significant form of living experience. A subsequent chapter links the LA’s Refresh Pulse with experimental data associated with Sleep and Consciousness. This widespread empirical evidence indicates that humans and perhaps other living systems naturally entrain to the Rhythms of Attention as identified by DSD. Later chapters illustrate an evolutionary and neurological connection with the LA. Both Posner & Dement’s models seem to have evolved to take advantage of the LA’s evolutionary potentials.
Summary
IT & AT are complementary
Let’s summarize our findings. Our Theory of Attention is a complement to Information Theory. Both theories are based in mathematical systems that deal exclusively with data streams. IT specializes in the exact transmission between machines of binary Information that has been deliberately stripped of meaning. In contrast, AT specializes in how Living systems extract meaning from data streams.
What sets RL apart from other types of Logic?
Redundancy Logic (RL) is a special form of logic that was derived from IT. What sets RL apart from other forms of logic?
Deduction can only draw Definitive Conclusions from Definitive Assumptions
Induction is employed as form of pattern recognition, i.e. inferring general patterns from specific examples. While pointing the way, Induction does not result in Definitive Conclusions. In contrast, Deduction can make Definitive Conclusions, but only if it operates upon Definitive Assumptions. If Deduction operates upon Ambiguous or Questionable Assumptions, the Conclusions are equally Ambiguous or Questionable.
Deduction cannot draw Definitive Conclusions in Living Realm
Deduction can be employed to make Definitive Conclusions regarding Mathematics, Material Realm, and Technology because Definitive Assumptions are possible in these arenas. However, only Ambiguous or Questionable Assumptions are possible in the Living Realm of Ideas and Behavior. This is due in part to the Innate Ambiguity of Words and the Interactive Feedback Loops associated with Living Behavior. Because of these innate features, Deduction cannot make Definitive Conclusions in the Living Realm.
Deduction requires support of Redundancy Logic in Living Realm
Because of this fragility, a single deductive thread needs support. This is where Redundancy Logic enters the picture. With enough redundancy in error-correcting codes, engineers can get as close as they want to an exact transmission of Information. Similarly with enough redundancy of the right type, living systems can also approach truth regarding reality.
RL primary form of Logic for Life, including Academia
For this reason, RL is the primary form of logic employed by living systems. Multiple senses are the most obvious form of redundancy. In the human realm, Academia employs 5 primary forms of redundancy to approach truth: 1) single logical threads, 2) collective consensus via journals, 3) empirical evidence, 4) experimentation, and 5) mathematics.
Point: Single Deductive Chain insufficient in Attention Realm
It is evident that a Single Deductive Chain is insufficient to establish truth, especially in the Living Realm. Multiple forms of cross-validation are required. This is the essence of Redundancy Logic.
Footnotes
1. This quotation from Claude Shannon is contained in The Information by James Gleick, Vintage Books, 2011, p. 221-2
2. Gleick’s The Information, p. 219
3. Grammatical Man, Jeremy Campbell, Simon & Schuster, New York, 1982, pp. 77-78