Section Headings
- The Appropriate Mathematics for the Job?
- Mathematics of Matter: Regular Equations obey Set Theory
- Absolute Essence, Set Theory & Deduction
- Living Behavior Lacks Absolute Essence
- Living Behavior: Dynamic Context, Feedback Loops & Reflexive Equations
Synopsis:
Why hasn't Material Mathematics been able to model living behavior? Could Life require a different type of mathematics – a mathematics that doesn't objectify her, but instead provides a language for her special features?
For centuries, mathematicians, scientists and philosophers assumed that there was only a singular mathematics that described a single universal truth. Brilliant thinkers utilized this singular mathematics to model material behavior. With the discovery of the Subatomic Universe in the 20th century, mathematician-scientists were forced to derive a different type of mathematics to characterize the behavior of this bizarre realm. Despite their awesome ability to make increasingly accurate predictions about material behavior, these two mathematical systems appear to be helpless before living behavior. Why?
According to our Theory of Attention, common sense and modern biology, living systems regularly engage in interactive feedback loops with their environment, both internal and external. We monitor our environment, assess the incoming data streams in relationship to internal states, and then adjust accordingly. We engage in this multistage reflexive process countless times throughout the day on micro and macro levels, both consciously and subconsciously.
Material Mathematics employs so-called ‘regular equations’. Regular equations obey traditional set theory. To join this exclusive club, equations can't contain themselves, i.e. reflexive feedback loops. Due to this innate deficiency, these so-called ‘regular equations’ can’t model the interactive feedback loops of living systems.
Life requires a different type of equation to characterize her behavior. The Living Algorithm embodies the interactive reflexive loops of living systems. As such, it is ideally suited for the job. However, due to its reflexivity, the equation does not obey the definitive laws of traditional set theory. Due to this non-conformity, we have deemed it Life’s disobedient equation.
The Appropriate Mathematics for the Job?
According to our Theory of Attention, Attention belongs to a realm of existence that is distinct from the Material Realms, i.e. Molecular and Subatomic. The justification for this audacious claim is that each of the realms has its own mathematics. These 3 unique mathematical systems are based in 3 mutually exclusive versions of reality. For example, the nature of space and time is totally different in each realm. Emergence doesn’t account for these extreme differences in the underlying structure of reality. Rather than a single Material Realm, we suggest that the Universe is better conceptualized as 3 interacting realms of existence. (For more, see the article: Attention & Matter: Interacting Realms of Existence?)
Different Math for each Realm
According to this line of reasoning, existence requires multiple types of mathematical systems to characterize its behavior. This statement evokes several questions, which this article attempts to answer.
Multiple Maths?
First, are there really multiple mathematical systems? Aren’t they just part of one unified system? Second, why does living behavior require a different type of mathematics than material behavior?
Specialists necessary
The notion that there is not one, but multiple mathematical systems might seem strange. It certainly violates a common understanding that there is only one mathematics. Yet common sense dictates that specialists are necessary. We have specialists, e.g. doctors, plumbers, and lawyers, to deal with the various aspects of our modern lives. We call a plumber, not a lawyer, to fix a clogged toilet. It is necessary to have the right specialist for the job at hand.
Need Mathematical Specialists:
Similarly, we need the correct type of mathematics for the job. One mathematics doesn’t fit all phenomena. For instance, the effort to employ material mathematics to characterize living decision-making seems doomed to failure – like hiring a doctor to fix your car. Instead of a singular and unified system of equations and formulas, each realm requires a mathematics that specializes in its unique aspect of existence.
Particles, Subatomics, Attention
In terms of our 3 realms of existence, the classical equations of traditional Newtonian Physics specialize in the behavior of the Molecular Realm, i.e. atoms and particles outside of an atom. The mathematics of Quantum Physics specializes in the behavior of the Subatomic Realm, i.e. the paradoxical subatomic entities on the interior of an atom. Yet another mathematical system, Data Stream Dynamics, specializes in the behavior of the Realm of Attention, i.e. living behavior in relationship to Attention.
3 Different Mathematical Types for 3 Different Features of Existence
The empirical data and patterns of each realm are strikingly different. Each realm seems to require a unique mathematical system to model or reflect these behavioral patterns. These 3 mathematical systems map territories that have vast differences.
Molecular and Subatomic: Complementary Realms requiring Unique Mathematics
The notion of differing realms with unique mathematical systems is not controversial in any way. After some initial battles, the scientific community almost universally shares the common consensus that the Molecular and Subatomic Realms belong to complementary realms of existence. These complementary realms come with mutually exclusive versions of reality that require two different types of mathematics.
Mathematics of Matter: Regular Equations obey Set Theory
If Life consists only of Matter, why doesn’t Material Mathematic work?
Up to here everyone agrees. The next step is as controversial, if not more so, than the step from one to two material realms. The miraculous successes in the material sphere led philosophers and scientists to the relatively obvious 3-step deductive chain:
1. Material Mathematics is able to accurately predict Material Behavior.
2. Life consists of Matter.
3. Then Material Mathematics should be able to accurately predict Living Behavior, which includes Attention.
Does Material Mathematics have a fatal flaw regarding Attention?
But as of yet, it can’t. If Life consists only of Matter, why isn’t Material Mathematics able to characterize Living Behavior? Is an insight just around the corner? Or does Material Mathematics have a fatal flaw that prevents it from ever making absolute predictions regarding Attention?
Material Mathematics: commonalities between Molecular & Subatomic Math
To address these questions, let us examine the Mathematics of Matter in more detail. Subatomic and Molecular Mathematics, as delineated, have many differences. However they also share some significant features that the Mathematics of Attention doesn’t have. The following discussion concerns these more general, yet shared features of the combined Mathematics of Matter.
Material Mathematics = Subatomic Mathematics + Molecular Mathematics
Material Mathematics makes exact predictions
This branch of mathematics is exact in that it can make precise predictions about material behavior. The appropriately called exact sciences, e.g. Physics, Chemistry, and Mechanics, are founded in Material Mathematics. Scientists and engineers can employ this type of mathematics to determine Matter’s behavior to any level of desired precision. Indeed scientists assume they can always make virtually exact predictions with the proper equations. As an indication of the exactitude of this branch of science, assumptions, theories, equations and measurements are thoroughly inspected and adjusted until discrepancies are resolved.
![]()
Automatic and Instantaneous Cause-effect Chains
Material Mathematics is based in automatic and instantaneous cause-effect chains. If ‘this x’ happens, then ‘that y’ always happens. Atoms and Subatomics always follow the rules of mathematics. No variance. When anomalies are uncovered, physicists tweak formulas and come up with different expressions that will account for the discrepancies. For all practical purposes, Matter remains completely obedient to the cause-effect chains delineated by Material Equations.
![]()
Material Mathematics based in Regular Equations
The Mathematics of the Material Realm that makes such precise predictions about the behavior of Matter has some significant features. It is based in what we will call Regular Equations, for reasons that shall be revealed.
![]()
Regular Equations obedient to Set Theory
Regular Equations, technically called well-founded functions, are special in that they adhere to traditional set theory. Set theory is based in the notion that entities are either inside or outside the box.
![]()
Regular Equations are inside the set theory box.

Set Theory enables precise predictions with approximation techniques
Traditional set theory has many marvelous features. These features enable scientists to make precise predictions about a wide range of phenomena. Engineers love one feature in particular. No matter how messy, i.e. complicated, an equation is, there are approximation techniques that enable engineers to obtain any level of precision from the function. These mathematically validated approximation techniques are invaluable in the real world of machines and computer technology.

Well-founded Functions, i.e. Regular Equations, obey Axiom of Regularity
To join this elite club of mathematics, an equation must have a few essential characteristics. There is one characteristic in particular that concerns the present discussion. Well-founded functions obey the axiom of regularity – hence their nickname, i.e. Regular Equations.
![]()
Regular Equations don’t include themselves – Not Reflexive
The most significant meaning of this axiom is that Regular Equations can’t include themselves, i.e. no self-referential feedback loops. Any equation that refers back to itself is not a Regular Equation.
![]()
Feedback Loops invalidate Approximation techniques
Self-referential feedback loops invalidate the above mentioned approximation techniques that are so invaluable to engineers.

Reflexive Equations don’t obey Axiom of Regularity
There is another class of equations that doesn’t obey the axiom of regularity, hence their nickname – disobedient equations. Although their technical name is recursive functions, we call them Reflexive Equations because this type of equation is based in self-referential feedback loops. In mathematical terminology, they contain themselves.
Scientists love Predictable Regular Equations & shun Unpredictable Reflexive Equations
Due to their set-based, absolute predictability, scientists love Regular Equations. Conversely, they shun Reflexive Equations because of their unpredictability. Traditional set theory along with the precise predictions and approximation techniques don’t apply to disobedient equations.
Mathematics of Matter excludes Reflexive Equations
No matter how hard they try; no matter how many recommendations they get, no matter how applicable they are to a wide range of situations/phenomena, these equations are excluded from Material Mathematics because they don’t adhere to traditional set theory.
Absolute Essence, Set Theory & Deduction
Why the Exact Fit between Regular Equations & Material Behavior?
Why do the Regular Equations of traditional set theory provide a virtually exact model for material behavior?
Matter’s content & behavior has Absolute Essence
Absolute essence. Both the content and behavior of Matter has an absolute essence. The foundations of our physical universe, i.e. atoms, electrons, photons, et al, always have the same content and always behave exactly the same under the exact same set of circumstances. The laws that apply to Matter’s behavior are absolutely true. This is why Matter is so predictable.
Absolute Content: Moleculars & Subatomics
For instance, the scientific community is in complete agreement that every hydrogen atom has the exact same content. The same holds true for the Subatomic Realm. Every electron has the exact same content. Moleculars, the particles of the Molecular Realm, and Subatomics both have an absolute content – no variation from hydrogen atom to hydrogen atom or electron to electron.
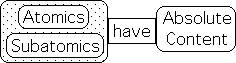
Individual Atoms & Collective Subatomics obey Absolute Mathematical Laws
Further every hydrogen atom behaves identically to every other hydrogen atom. Each and every Molecular particle obeys the mathematical laws of the Molecular Realm. The Subatomic Realm is a little different. While individual atoms are totally predictable, individual subatomics, e.g. photons, are unpredictable. However, collectively photons obey the same mathematical laws of the Subatomic Realm in exactly the same way every time. For all practical purposes, Subatomics are just as obedient to mathematics as are Moleculars. Put simply, Individual Moleculars and Collective Subatomics obey absolute mathematical laws.
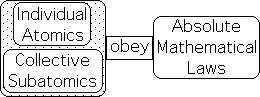
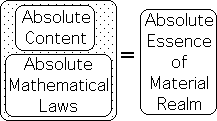
Absolute Essence of Matter = Absolute Content + Absolute Mathematical Laws
Both Moleculars and Subatomics have absolute invariable content and obey absolute mathematical laws. The absolute essences of the Material Realm consist of the absolute content and the absolute mathematical laws of the Subatomic and Molecular Realms.
Major Scientific Achievement Identifying Essence of Matter
The gradual discovery that matter has an absolute essence in terms of both content and behavior was a major scientific achievement. The miracles of material science are based upon identifying the absolute essences of our material world. These determinations have enabled the marvels of modern technology.
![]()
Why is establishing Essence so crucial?
Why is establishing essence so crucial?
Set Theory requires Essence to determine if something inside or outside the box
Absolute essence is a crucial feature of set theory. It determines whether the entity is inside or outside of the box, i.e. the set. If it has certain characteristics, it is inside the box and obeys certain laws. If the entity doesn’t have these characteristics, then it is outside the box and the same laws don’t apply.
![]()
Determining Absolute Essence enables Predictions
For example, a water molecule always consists of 2 hydrogen atoms and 1 oxygen atom in a certain configuration. Once scientists have determined what the essence of the molecule is they can make absolute predictions about its behavior, e.g. how it interacts with other molecules. Determining absolute essence enables scientists and engineers to make useful predictions. Ultimately the predictability of matter’s absolute essence has made it possible to tap into unimaginable energy sources that transform our world.
Once Essence established then Regular Equations apply
Why? If absolute essence is established, then Regular Equations apply. These Regular Equations belong to the vast interlocking network of Material Mathematics. Traditional set theory provides additional complexity and understanding to the interactions.
![]()
Deduction applied to Assumptions to reach necessary Conclusions
Images 5>10 in RlmChoice1b Images Folder
Absolute essence is important for another reason. It is the basis Deductive Logic. Deduction is also absolute. Assumptions are made. Conclusions follow of necessity. There is no debate. Euclid’s Elements provides the classic example. By applying Deduction to distinct definitions and postulates (assumptions), Euclid generated the permanent mathematical structure of geometry. No challenges.
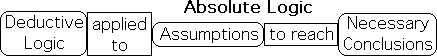
Deductive Assumptions based in Absolute Essence
The assumptions of Deduction are founded in absolute essence. These assumptions can’t be dependent upon external conditions. They can’t be true in certain situations and false in others. Deduction is applied to absolutely true assumptions to arrive at definitive conclusions. Everything, the entire logical foundation crumbles without absolute essence. Necessary deduction only applies to absolute essence.
![]()
Math based in Deductive Logic
All mathematical systems, including Material Mathematics, are based in deduction applied to assumptions. Mathematics applies deduction to the absolute essence of numbers. This process yields absolute mathematical truths.

Mathematical Truths matched to Absolute Essences of Material Realm
Scientists successfully match these mathematical truths with the behavior of the absolute essences of the material world. In such a way, they are able to make precise and unvarying predictions about Matter. Due to this utility, the scientific community has devoted a considerable amount of time and energy attempting to correctly identify essences.
![]()
Correctly Identifying Matter’s Absolute Essence enables Set Theory, Deduction & Regular Equations
For the material world, scientists have been incredibly successful in the determination of absolute essences. Identifying absolute material essences is the key ingredient that enables Set Theory, Deduction, and Regular Equations. These factors in turn enable the exact predictability of the Material Realm. Living behavior is another story.

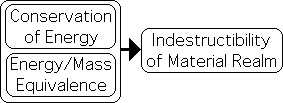
Conservation of Energy always true in Material Realm
Let us provide a concrete and relevant example of the absolute mathematical laws that are employed to predict material behavior. The conservation of energy is one of the immutable laws of the Material Realms. Energy is never used up. However it is frequently transformed from one form to another, perhaps from mechanical to electrical to heat energy. This law is independent of context. It is always true. This law is one of the primary foundations (an absolute essence) of Material Mathematics.
Matter/Energy are One, E = mc2 always true in Material Realm
Another mathematical law that is always true in the Material Realm is Einstein’s E = mc2. This equation indicates that Matter can be converted to Energy and vice versa. Matter and Energy are just different sides of the same coin. This mathematical law is another absolute essence of Material Realm – something that can be counted upon in virtually all situations. The absolute truth of both equations is the basis of countless traditional set-based Regular Equations with all their predictability.
Combined: Material Realm indestructible
When combined, the two laws indicate that the Material Realm is conserved – no degeneration. While there might be varying amounts of Matter and Energy, the quantity of the Matter-Energy synergy in the Universe is a constant. Although going through transformations from one form to another, the Material Realm is indestructible – an absolute and unassailable essence. As a simple example, an individual atom can last for billions of years.
Nobody doubts truth of equations and their implications
These equations along with their assumptions have been validated so many times in such many different contexts that virtually nobody doubts that they and their implications regarding the Material Realm are absolutely truth.
Living Behavior Lacks Absolute Essence
Living Behavior has Relative, not Absolute, Essence
Due to their amazing successes with material behavior, the scientific community has attempted to apply the same model to living behavior. Yet, scientists have searched in vain for the absolute essences of, for instance, human interactions. For human behavior, rather than absolute essence, they have learned to be content with relative essence, which means the boundaries are probabilistic.
Regular Equations require Absolute Essence
Unfortunately, the Regular Equations of traditional set theory only apply to absolute essences. Anything less, i.e. relative essence, invalidates the deductive process. Rather than the definitive conclusions of deduction, scientists can only make probabilistic statements regarding living behavior.
Why not Living Behavior?
Why the difference between Life and Matter? Why isn’t Living Behavior subject to the absolute laws of Material Behavior?
If Life only Matter, Regular Equations should apply, but don’t
If Life only has a material component, then Regular Equations of Material Mathematics should apply. Many scientists maintain the hope that someday someone will uncover some set-based formulas that apply to human behavior. So far that has not been the case.
Could Life have immaterial component associate with Choice & Info?
If living behavior has resisted a material explanation, could it be that Life has a non-material component? Could it be that this non-material component is associated with our ability to choose and by extension our relationship with Information? Is it possible, maybe even probable, that living, and thereby human, behavior is motivated, as least in part, by this non-material Realm of Attention?
Why no Regular Equations for Choice? Possibly immaterial component
Regular Equations certainly apply to Life’s material component. In fact, the scientific community has uncovered countless traditional set-based equations that apply to the Material Realm. Why haven’t scientists been able to uncover a single Regular Equation that applies to Life’s seeming ability to choose between alternatives – the Realm of Attention?
Life’s immaterial component lacks absolute essence because of death
Simply speaking, Life’s Realm of Attention lacks absolute essence. Why? The reasons surround the notion of Death.
Death separates Life from Matter; Matter, Immortal & Indestructible; Life, Mortal & Transient
Death differentiates Living Matter from Non-living Matter. As the Buddha says and Science has confirmed, our Realm of Existence, both Living and Material, is in a constant state of flux. Yet there is huge difference between the flux of Living and Non-living Matter. Although it goes through a virtual infinity of transformations, the Realm of Matter is indestructible. It never really dies or could be said to degenerate. The Material Realm is immortal and indestructible. In contrast, the Living Realm is mortal and transient. This is due to the inevitability of Death for living systems.
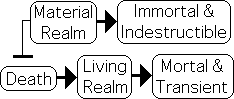
Why the difference? Death.
Life & Death inextricably linked
The notion of death permanently separates the two realms of existence, as only living entities can die. Life and Death are inextricably linked. At every moment, an uncountable number of living systems are both being born and are dying. After birth, Life heads inevitably towards Death. No living system is able to avoid this perpetual cycle.

Living Systems are collection of molecules that want to maintain integrity
Each and every living system from cells to humans is a cohesive collection of molecules that somehow wants to maintain its integrity. More importantly, after a limited duration, these same molecules change course. Rather than sticking together, they decide to go their merry ways. With ultimate death, these same atoms & molecules that have clung so desperately to Life suddenly disband forever. This process happens relatively rapidly. That which was warm, animated and organized becomes cold, lifeless and disorganized.
Quotation: Dr. Thomas, organization, physical difference between Living & Non-Living Matter
The process of maintaining the cohesion of a particular group of well-organized atoms and molecules does not occur in the realm of Non-Living Matter. In his best-selling book, The Lives of a Cell, Dr. Lewis Thomas, a noted mainstream biologist, affirms this physical difference between Life and Matter:
“Even more astounding is our statistical improbability in physical terms. The normal, predictable state of matter throughout the universe is randomness, a relaxed sort of equilibrium, with atoms and their particles scattered around in an amorphous muddle. We, in brilliant contrast, are completely organized structures, squirming with information at every covalent bond. We make our living by catching electrons at the moment of their excitement by solar photons, swiping the energy released at the instant of each jump and storing it up in intricate loops for ourselves.”1
Life Force: organizational, non-entropic
Just as there are powerful nuclear forces that bind the nucleus of an atom together, there must be some kind of, what we shall call, Life Force that holds the intricate system of molecules together against all odds.
![]()
Death implies Life Force, something that bind’s atomic collection together
Death implies this Life Force. The force of gravity binds us to the earth; nuclear forces bind protons and neutrons in the nucleus to maintain the atom’s integrity. In similar fashion, a Life Force is required to bind a specific collection of atoms and molecules together in order to maintain the cell’s integrity.
![]()
Cells: Cohesive Molecular System
Both Gravity and the Nuclear forces are attractive. Gravity is the force that attracts two masses towards each other. Nuclear forces attract protons and neutrons together. Both the Universe and individual atoms would disintegrate as cohesive systems without these natural forces. In similar fashion, Cells would disintegrate as a living system without a Life Force.
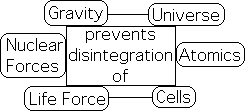
While the other forces are attractive, the Life Force is much more than simply an attractive force. How does the Life Force do its job?
Life Force, organizational, non-entropic
The Life Force is an organizational, non-entropic, force. While relying on the attractive feature of gravity and the nuclear force, the Life Force must also organize molecules in a specific fashion if they are to survive as a cohesive unit. In fact, its primary purpose is maintaining the cohesion, i.e. survival, of the molecular complex that is the basis of single cell or multi-cellular Life. It requires a variety of components to maintain the Cell’s integrity. Once this Life Force leaves, the molecules, with nothing to organize them as a unit, also disperse.
![]()
Life Force Maintains Homeostasis to Survive
What is the focus of the organizational process? To preserve the cohesiveness (survival) of the molecular collection and thereby forestall dispersion (death), the mysterious Life Force must maintain the homeostasis of the living system, whether cell or human. For instance, organisms must constantly regulate input and output, e.g. food and waste, in order to survive.
![]()
Requires Interaction with Environmental Info
Maintaining homeostasis requires an interaction with environmental information both internal and external. To facilitate this process, Living Matter engages in interactive feedback loops with environmental Information. The feedback loop is between internal feeling states & relevant information.

For instance, the organism might feel hungry or satiated. This feeling state determines whether food information is significant or not. When hungry, the data streams related to sustenance are of utmost importance. The content of the data stream, i.e. food, is less important than the context of data stream, i.e. hungry or satiated.
Maintaining homeostasis is a dynamic process that depends upon context.
Maintaining homeostasis is a dynamic process that depends upon context. Even the simplest cells become hungry, consume sustenance and then become satisfied. This dynamic process is repeated innumerable times for every form of Life. Food motivates the organism when it is hungry, but not after this urge is satisfied. The context, not the content, determines significance for the organism. Contextual processes are more important than absolute content in determining living behavior.
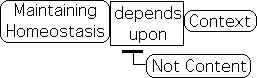
Contextual Nature of Truth undermines Absolute Essence
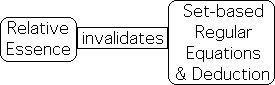
The contextual nature of truth undermines the notion of absolute truth. Without absolute truth, there is no absolute essence. Without absolute essence, Deduction and Regular set-based Equations are inoperable.

Interactive Feedback Loops invalidate Regular Equations
Living systems must engage in self-referential, interactive feedback loops with environmental Information in order to maintain homeostasis and survive. In contrast, Regular Equations, by definition, do not contain themselves, i.e. no self-referential feedback loops. Due this limitation, how could Regular Equations possibly mimic, model or emulate these interactive feedback loops with Information that Life requires to survive? In contrast, Regular Equations does a great job with Non-living Matter, which doesn’t engage in feedback loops to survive as it never dies, just transforms from one state to another.
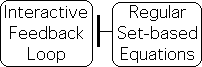
Set-based Logic with Regular Equations imprecise fit w/Living Realm
As organisms are continually becoming something new, they have no absolute essence. Based in the absolute truth of the assumptions, deductive logic is invalidated as a means of investigation. As they are constantly engaging in self-referential feedback loops with the environment, Regular Equations with their set-based logic are not applicable to this feature of Living Matter. Based in deduction applied to the absolute essences of the material world, the Mathematics of Matter with its Regular Equations is inappropriate for the dynamic, contextual processes of the Living Realm of Attention.
Need Another Type of Mathematics to characterize Living Realm
Due to the inadequacy of Material Mathematics, could it be that another type of mathematics is needed to characterize the Living Realm? Living processes entail ‘becoming’ due to interactive feedback loops. Could a mathematics that encompasses these features be a better fit?
Is there a Different Type of Math that applies to Choice Realm?
Every form of mathematics employs invariable deduction upon the absolute essences of numbers to come up with absolute truths. Material Mathematics with its set-based Regular Equations matches these absolute numerical truths with the absolute essences of the material world to come up with absolute truths that apply to the Material Realm. Could the absolute truths of a different type of mathematics match the dynamic processes of the Living Realm? What type of mathematics would that be?
Living Behavior: Dynamic Context, Feedback Loops & Reflexive Equations
Living & Non-Living Matter: Identical Content but Differing Behavior
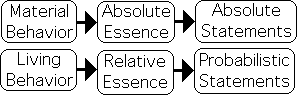
Before addressing these questions, let us review our current understanding. The content of Living and Non-Living Matter is identical, i.e. Molecular particles and Subatomic entities. This equivalence doesn’t seem to apply to behavior. The behavior of Non-Living Matter is entirely predictable, while the behavior of Living Matter is unpredictable. Engineers and scientists can make definitive statements regarding the outcome of events regarding exclusively material systems, while they can only make probabilistic statements regarding living systems.
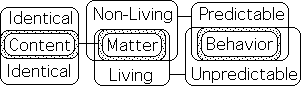
Regular Equations for Material, not Living, Behavior
The scientific community employs Regular Equations to characterize and make precise predictions about the behavior of Non-Living Matter. Scientists have not been able to employ these same set-based equations to characterize or predict the behavior of Living Matter.
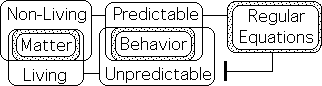
Life’s Predictable Material Component
We must qualify or refine this last statement. Scientists can make absolute predictions about Life’s exclusively material component, i.e. the Moleculars and Subatomics. As would be expected, Regular Equations are employed for this task.
Life’s Immaterial Component Unpredictable
Living and Non-Living Matter have identical content and Matter is entirely predictable. How do we account for Living Matter’s unpredictable nature? One camp holds that scientists will eventually uncover some Regular Equations that are able to characterize and predict the behavior of Living Matter, just as they do Non-Living Matter.
There is another alternative. Let us suppose that Living Matter has an immaterial component that is not based in absolute essence. If a system lacks absolute essence, Regular Equations do not apply. If Life does indeed have two components, i.e. material and immaterial, this would account for the inability of Regular Equations to characterize Living Behavior.
Regular Equations can’t deal with Life’s Immaterial Component
Although Regular Equations accurately characterize and predict Life’s material component, they have fallen short with Life’s immaterial component. Is there another kind of Mathematics that might be able to characterize Life’s immaterial behavior? What type of mathematics would that be?
Reflexive Equations contain themselves – don’t obey Axiom of Regularity
Regular Equations by definition obey the Axiom of Regularity. These obedient equations don’t contain themselves. There are other types of equations that don’t obey the Axiom of Regularity in that they contain themselves. Because they don’t follow the rules of traditional set theory, let us call these Reflexive Equations.
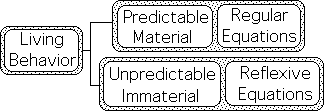
2 Components of Living Behavior: Material – Regular Equations; Immaterial – Reflexive Equations
As mentioned above, living systems must engage in an interactive feedback loop with environmental Information in order to survive. These feedback loops are self-referential in that they regularly reference internal states in order to place relative value upon sensory data streams. While Regular Equations match Life’s predictable Material component, we suggest that self-referential Reflexive Equations would be a better fit with Life’s self-referential immaterial component.
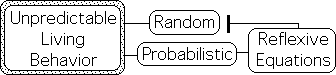
Living Behavior: Random & Probabilistic Component
If Living Behavior is truly unpredictable, what is the function of Reflexive Equations? Living Behavior seems to have a probabilistic component that is somewhat predictable. Indeed modern psychology specializes in making probabilistic claims about Living Behavior. However, it does appear that there is a random component that is entirely unpredictable. Is it possible that Reflexive Equations could model the probabilistic feature of Living Behavior? The evidence indicates that the answer is yes.
Probabilistic Behavior: Subatomics vs. Living
What is the difference between the probabilistic behavior of Subatomics and Humans? Individual Subatomics are entirely unpredictable. Yet Regular Equations are able to make absolutely precise predictions regarding the behavior of large numbers of Subatomics. Rather than precise predictions, Regular Equations are only able to make rough probabilistic predictions regarding human behavior both individually and collectively. More importantly, Regular Equations reveal very little, if anything, about the underlying patterns of human behavior. Could Reflexive Equations serve this function?
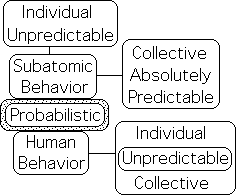
The behavior of both living and subatomic entities is probabilistic. Yet this is where the similarity ends. The behavior of both Subatomic and Living entities is unpredictable on the individual level. In contrast to this unpredictability, the collective behavior of Subatomic entities is completely (absolutely) predictable with Regular Equations. In contrast to this complete predictability, only probabilistic statements can be made about the collective behavior of Living entities.
Regular Equations reveal the internal laws of material behavior. Is it possible that Reflexive Equations could reveal the inner laws of living behavior?
It seems that there is a significant difference in kind, not degree, between the innate nature of Material and Living Behavior – the one ultimately definitive, the other probabilistic. We further suggest that this difference is due to the possibility of Choice in the Living Realm. The very potential for Choice, no matter how constrained, has the possibility, even probability, of undermining the predictability of Living Behavior. Rather than the absolute certainty of the predictions regarding Material Behavior, Choice turns Living Behavior into a probabilistic affair. In terms of predictability, the probabilistic nature of Choice differentiates the Living from the Material Realms.
According to this analysis, decision-making is based upon a ‘monitor and adjust’ relationship with the Information contained in data streams. This monitor-adjust relationship is based in interactive feedback loops between organism and environment. These self-referential feedback loops are outside the box of traditional set theory, hence Regular Equations as well.
Both the monitor and adjust aspects of the decision-making process require analytics in order to maintain the homeostasis that is foundation of survival and integrity of the organism. Because of the immortal and indestructible nature of the Material Realms, Regular Equations are closed. They apply in all circumstances, regardless of context. Due to their closed nature Regular Equations don’t respond to external data. As such, they can’t supply the ongoing, up-to-date, weighted analytics that living systems require to both monitor and adjust to environmental data streams. Ultimately, the innate features of the entire and vast class of Regular Equations render them incapable of replicating or modeling Life’s monitor-adjust relationship with Information.
Lacking some innate features, the infinite set of Regular set-based Equations can’t fulfill Life’s qualifications for a Mathematics of Choice. Is Life doomed to a solitary existence without a mathematics to characterize her seemingly erratic behavior? Or is there a Disobedient Equation that can fulfill the job requirements?
We offer a candidate for the position – the Living Algorithm. If the endless class of Regular Equations is inadequate, how can a single algorithm fulfill the complex computational needs of living organisms? Unlike Regular Equations, the Living Algorithm (LA) is a Disobedient Equation that is self-referential and open to external information. As such, it is perfectly suited to Life’s monitor-adjust process. The LA specializes in supplying ongoing, up-to-date, weighted analytics regarding any data stream. An abundance of evidence from a variety of diverse fields supports the hypothesis that Life employs the LA as a computational interface with the Information contained in environmental data streams. As Life’s computational tool, the Living Algorithm generates the Mathematics of Choice.
Matter & Life different types of Mathematics: Continuous vs. Data Streams
The Mathematics of Choice only applies to living systems. The mathematics that characterizes Matter so perfectly is fundamentally different from the mathematics associated with Life’s decision-making process. As mentioned, Material Mathematics is based upon a continuous flow of information, while Choice Mathematics operates upon discretized data streams.
Matter: closed and regular, obeys set theory
But this is just the tip of the iceberg. The Mathematics of Matter is founded upon closed and regular equations. Due to continuity, i.e. no breaks, the equations are closed to outside information. Further regular equations never refer back to themselves. Because of this feature, they obey the laws of traditional set theory – inside or outside of the box.
LA: an open recursive function, disobedient to set theory
In contrast, the LA is a recursive function, i.e. self-referential/reflexive, in that it refers back to itself. Further it is open to external information. This is why it could be so useful to living systems. Due to its self-referential nature, the LA does not obey traditional set theory. This means that the processes it characterizes are less predictable. Despite or perhaps because of its disobedience, the LA has a lot to tell us about the disobedient Living Realm of Attention.
Mathematics of Choice reveals underlying Patterns
What can be said about the dynamic processes of something that has no absolute essence? As mentioned, Material Mathematics matches the absolute numerical essences of Regular Equations with the absolute essences of the material world to make precise predictions. The Mathematics of Choice matches the absolute numerical essences of Reflexive Equations with living behavior to reveal underlying patterns.
Realm of Attention, no absolute essence only patterns
The Mathematics of Matter is based in Regular Equations and applies perfectly to the absolute essences of the Material Realm. The Mathematics of Choice is based in a Reflexive Equation and applies approximately to the dynamic and contextual processes of the Realm of Attention. Both types of Mathematics employ deductive logic upon absolute numerical essences to come up with intriguing relationships.
Matching Mathematical Patterns with Behavioral Patterns
Material Mathematics can employ this same deductive logic with the absolute essences of the Material Realm. Because there are no absolute essences in the Living Realm of becoming, deductive logic with the Regular set-based Equations are not applicable. Instead, the dynamic process of becoming requires pattern recognition – matching the mathematical behavior of the LA, a disobedient equation, with living behavior.
Contextual Feedback Loops affinity between LA and Living Behavior – not Regular Equations
Because Regular Equations are set-based rather than based in feedback loops, there is little, if any, affinity with Living Behavior. Because Regular Equations can’t be self-referential by definition, it is almost impossible for there to be any kind of match whatsoever. Could this be why equations relating to Living Choice have eluded the brilliant minds of Material Mathematics? As both Living Choice and the LA are based in contextual feedback loops, there is an affinity between living behavior and the LA’s mathematical behavior. Because of this mutual affinity, there is a better chance of a match between mathematics and living behavior associated with Choice. The evidence suggests that this is so.
Summary: Math of Matter applies to Life’s material component
Let us summarize our findings. Living systems have a material component that is best characterized by the Mathematics of Matter with its Regular Equations. Living systems also have an immaterial component that Material Mathematics cannot address.
Math of Choice applies to Life’s immaterial component
Decision-making is the root of living systems’ immaterial component. Life’s ability to choose between alternatives is based on a computational relationship with environmental Information. According to our hypothesis, the Living Algorithm provides the computational basis of this relationship with Information. The Living Algorithm generates a Mathematics of Choice that is applicable to Living Behavior.

Significance of Mathematics of Choice?
Let us suppose that the Mathematics of Choice does indeed apply to Living Behavior. Is this unusual type of mathematics anything thing more than computational tool? Is computation the extent of its utility or does it have any greater significance? Could this mathematics reveal the underlying structure of our relationship with Information?
Mathematics of Choice: Symbolic Logic to reveal underlying structure of Living Behavior
Scientists employ the symbol logic of Material Mathematics to understand the underlying structure of Material Behavior. We employ the symbolic logic of Choice Mathematics to understand the underlying structure of Living Behavior. Rather than focusing upon the absolute essences of Matter, the mathematics focuses upon the dynamic processes associated with Living Choice. In the attempt to make sense of the synergy between the mathematical structure and empirical data, we came up with some startling and significant conclusions.
Mathematics of Choice: Process of Living Behavior has Different Type of Solution
What type of solutions can we expect from the Mathematics of Choice? The patterns of the dynamic processes associated with Living Choice are quite different than the patterns of Matter’s static essences. Accordingly, the Mathematics of the Choice is different in kind rather than degree from the Mathematics of Material Essences. Due to these differences, the types of solutions are also different. Absolute essences have definitive results; dynamic processes have relative results.
Questions: Evidence for LA hypothesis
What possible efficacy could relative results have? How could our relationship with the Information contained in data streams translate into action or non-action in the Molecular Realm that we inhabit? Is it possible that the immaterial Realm of Attention exerts an influence upon the immaterial Subatomic Realm, which in turn exerts a mysterious effect upon our Molecular Realm?
Read on for plausible answers
We don’t really know. Read on to find some plausible answers and to evoke some new questions.
Footnote
1The Lives of a Cell, Lewis Thomas, 1974, Bantam Books, p. 165. Among the many credentials of his notable career in biology with a focus upon immunology, Dr. Thomas was a member of the National Academy of Sciences.